10 Problems 2
Week 4
Problems class questions will be displayed during the class. You do not need to do these in advance of the problems class. The questions will be published the day before the problems class so you can take a look at them if you need to.
10.1 Sliding drink along a bar
The barman in a local nightclub prides himself in being able to slide any drink along the bar so that it comes to rest exactly opposite the correct customer. The coefficient of kinetic friction of the bottom of a glass on the bar is 0.25. If he slides a cocktail to a customer a distance of 3 m along the bar, at what speed must he release the glass from his hand?
The vertical forces balance in this problem. The friction force acts horizontally and results in the deceleration of the particle (glass containing drink).
In order to work out the friction force, we need the normal reaction which is equal to the particle’s weight. Once we know the acceleration, the relationship between the initial speed and the distance travelled can found using SUVAT.
The normal reaction is \(\mu_k mg\) so the acceleration is therefore \(-\mu_k g\). The distance travelled before coming to rest is found from \[ u^2 + 2as = 0 \] for an initial speed \(u\). So we have \[ u = \sqrt{2 \mu_k g s} = \sqrt{2 \times 0.25 \times 9.81 \times 3.0} \text{ m s}^{-1} = 3.8 \text{ m s}^{-1} \]
10.2 Tensions in climbing ropes
A climber of mass 65 kg is in equilibrium with their feet against a rock surface inclined at \(\theta = 40^\circ\) to the horizontal, and is supported by a rope running parallel to the rock face. Draw a diagram showing the forces acting on the climber. Find the tension in the rope. (Assume the force of the rock on the climber is at right angles to the surface.)
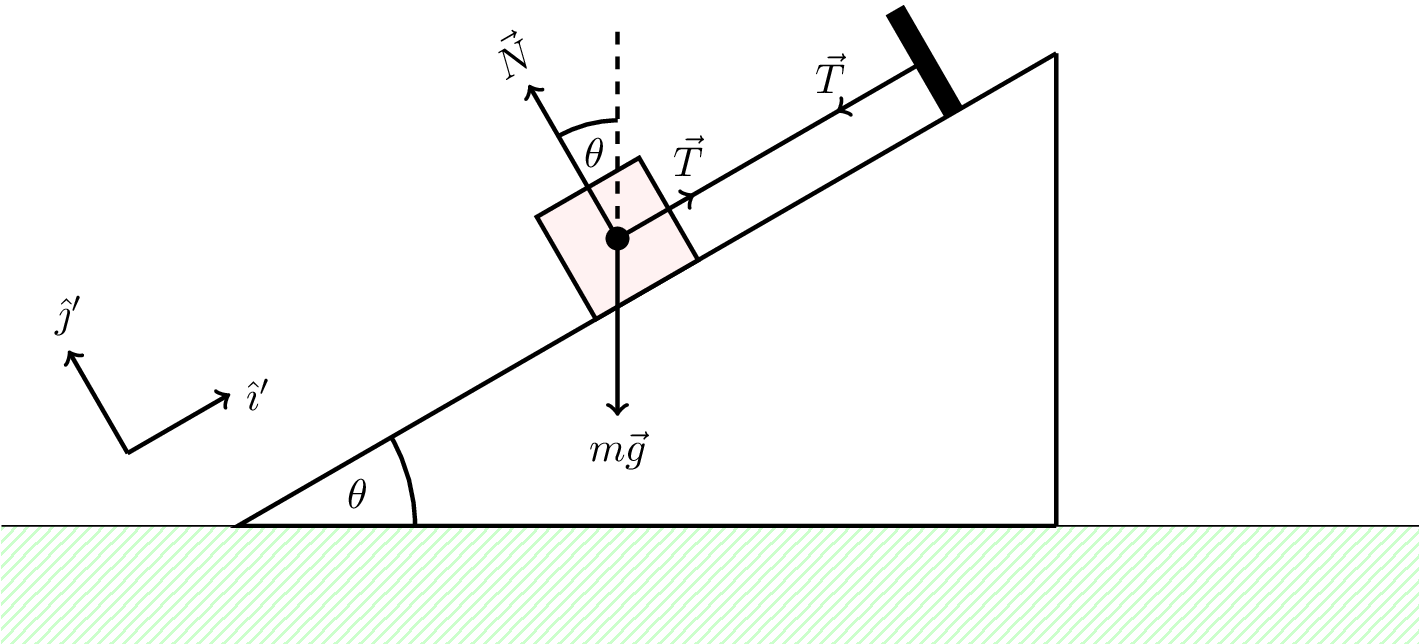
This is a case where a little thought, and careful choice of axes, can save a lot of work. Consider Figure 10.1 and resolve the forces parallel and perpendicular to the incline.
Parallel to \(\hat{\imath}'\) we have \[ T - mg \sin \theta = 0 \] Parallel to \(\hat{\jmath}'\) we have \[ N - mg \cos \theta = 0 \] We only need the first of these expressions to determine the tension in the rope, \(T\), \[ T = mg \sin (40) = 410 \text{ N} \]
Note: you can also solve this problem resolving the forces horizontally and vertically. However, resolving parallel and perpendicular to the plane is easier in this case.
10.3 Work done in a lift
A lecturer takes the main lift from the ground to the fourth floor in the Physics building. The lift exerts a force on the lecturer of 800 N for the first 0.45 m of travel. For the next 17.1 m the force is equal to the lecturer’s weight, 772 N and for the last 0.45 m it is 744 N. Find:
- The total work done by the lift.
- The total work done by gravity.
- The final kinetic energy of the lecturer.
The work done by the lift is \(800 \times 0.45 = 360 \text{ J}\) during the first 0.45 metres; 13.2 kJ over the next 17.1 metres and 334.8 J during the last 0.45 metres. Total work done is 13896 J.
The weight of the lecturer is \(mg = 772 \text{ N}\). The work done by gravity is \(-772 \times 0.45 \text{ J} = -347.4 \text{ J}\) during the first and last sections of the journey, and \(-13.2 \text{ kJ}\) in the middle section. Total work done is \(-13896 \text{ J}\).
So the total work done is \(12.6 \text{ J}\) in the first section, zero in the middle and \(-12.6 \text{ J}\) in the last section. Overall the total work done is zero, so the final kinetic energy of the lecturer must also be zero.
10.4 Work done by force not parallel to displacement
A 2 kg object is given a displacement \(\vec{s} = 3\hat{\imath} + 3\hat{\jmath} + 2\hat{k} \text{ m}\) along a straight line. During the displacement, a constant force \(\vec{F} = 2 \hat{\imath} + \hat{\jmath} + \hat{k} \text{ N}\) acts on the object.
- Find the work done as the particle experiences this displacement.
- Find the component of \(\vec{F}\) in the direction of the displacement.
To find the work \(W\) \[ W = \vec{F} \cdot \vec{s} \] \[ = (2 \hat{\imath} + 1 \hat{\jmath} + 1 \hat{k}) \cdot (3 \hat{\imath} + 3 \hat{\jmath} + 2 \hat{k}) \text{ N m} \] \[ = 6 + 3 + 2 \text{ J} = 11 \text{ J} \]
To find the component of \(\vec{F}\) in the direction of \(\vec{s}\), \(F_\parallel\), we use the fact that \[ \vec{F} \cdot \vec{s} = |\vec{F}| |\vec{s}| \cos \theta \] We want \(F_\parallel = |\vec{F}| \cos \theta\), which is \[ F_\parallel = \frac{|\vec{F}| |\vec{s}| \cos \theta}{|\vec{s}|} = \frac{\vec{F} \cdot \vec{s}}{|\vec{s}|} = \frac{W}{|\vec{s}|} \] \[ |\vec{s}|^2 = 3^2 + 3^2 + 2^2 \text{ m}^2 = 22 \text{ m}^2 \] \[ F_\parallel = \frac{11}{\sqrt{22}} \text{ N} \]
10.5 Heavy blocks colliding in 1D
A 2.0 kg block moving to the right with a speed of \(5.0 \text{ m s}^{-1}\) collides with a 3.0 kg block that is moving in the same direction at \(2.0 \text{ m s}^{-1}\). After the collision, the 3.0 kg block moves to the right at \(4.2 \text{ m s}^{-1}\). Find
- the velocity of the 2.0 kg block after the collision.
- the coefficient of restitution between the two blocks.
We use momentum conservation here. Since it is a one-dimensional problem and we are given the final speed of one of the particles, as well as the initial conditions, we can solve the problem.
Initial momentum of the system is \[ (2 \times 5 + 3 \times 2) \text{ kg m s}^{-1} = 16 \text{ kg m s}^{-1} \] The final momentum of the 3 kg block is \[ (3 \times 4.2) \text{ kg m s}^{-1} = 12.6 \text{ kg m s}^{-1} \] So the final speed of the 2 kg block is \[ \frac{3.4}{2} = 1.7 \text{ m s}^{-1} \] This result is positive so the block is still moving to the right after the collision.
To find the coefficient of restitution we look at the relative speed before and after the collision. Before the collision it is \[ (5 - 2) \text{ m s}^{-1} = 3 \text{ m s}^{-1} \] Afterwards the relative speed is \[ (4.2 - 1.7) \text{ m s}^{-1} = 2.5 \text{ m s}^{-1} \] So the coefficient of restitution is \[ e = \frac{2.5}{3} = 0.83 \]
10.6 Bonus question: Sailing boat in light wind
A sailing boat is oriented in a direction \(2 \hat{\imath} + 3 \hat{\jmath}\) on the surface of a lake, and its sail experiences a force from the wind of \(-50 \hat{\imath} + 250\hat{\jmath} \text{ N}\). You can assume the boat experiences no drag in the forward-aft direction, and that the keel provides sufficient resistive force against the water that any net motion of the boat is forwards. You can also assume the boat remains upright.
- Draw a free body diagram of the forces acting on the boat. What is the direction of any horizontal force the boat exerts on the water?
- Assuming the boat has mass 43 kg and the sailor has mass 78 kg, what is the magnitude of the acceleration of the boat?
A sensible diagram will have the force of the wind \(\vec{F}_w\) and the resistance of the boat. In the absence of any other drag, the resistance force of the boat should only point perpendicular to the direction of travel of the boat, and will oppose the component of Fw perpendicular to the keel i.e. \(\vec{F}_k\). The resultant force on the boat is parallel to \(\hat{n}\) i.e. \(\vec{F}_b\). This is shown in Figure 10.2.
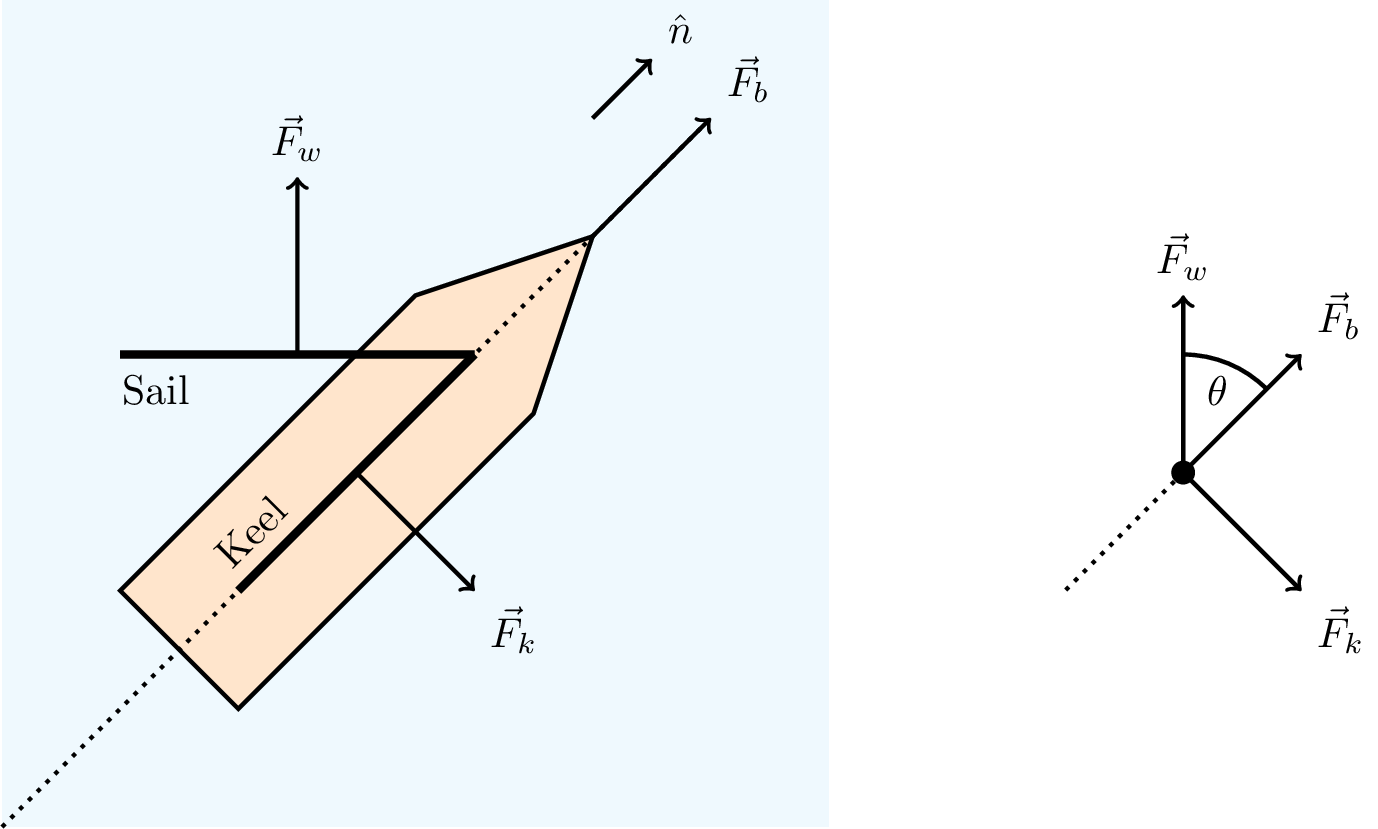
Using Newton’s second law \[ \vec{F}_w + \vec{F}_k = \vec{F}_b = m \vec{a} \] In the direction of the boat the only force acting is \[ F_w \cos \theta = F_b = ma_b \] i.e., we need to work out the component of \(\vec{F}_w\) in the direction the boat is pointing. \[ F_w \cos \theta = \vec{F}_w \cdot \hat{n} = \vec{F}_w \cdot \frac{\vec{n}}{|\vec{n}|} \] \[ = \frac{(-50\hat{\imath} + 250\hat{\jmath}) \cdot (2\hat{\imath} + 3\hat{\jmath})}{\sqrt{2 \times 2 + 3 \times 3}} = 180 \text{ N} \] Then we use \(F_b = ma_b\) with \(m = 43 + 78 = 121 \text{ kg}\). Hence \[ a_b = 1.49 \text{ m s}^{-2} \]