14 Workshop 1
Week 3
14.1 Part 1 - Preliminary questions
Formative (i.e., not assessed), for practice, and does not need to be submitted
These first questions are designed as revision of some of the maths you need during the mechanics course: calculus and vectors. It is always helpful to practise these techniques as they often appear in other parts of Physics!
14.1.1 Velocity to position
The velocity of a particle is given by: \[ \vec{v} = (5t\hat{\imath} + 6t^2\hat{\jmath} + 3\hat{k}) \text{ m s}^{-1} \] where the numeric constants carry appropriate dimensions. Find an expression for the position vector of the particle \(\vec{r}(t)\), given that \(\vec{r}(0) = (3\hat{\imath} + 2\hat{\jmath} + \hat{k}) \text{ m}\).
We need to integrate \[ \vec{v} = \frac{d\vec{r}}{dt} \] to get \(\vec{r}(t)\). \[ \vec{r} = \int \left( 5t\hat{\imath} + 6t^2\hat{\jmath} + 3\hat{k} \right) dt \] \[ \vec{r} = \left( \frac{5}{2}t^2\hat{\imath} + 2t^3\hat{\jmath} + 3t\hat{k} \right) + \vec{c} \] where \(\vec{c}\) is a constant vector. We can find \(\vec{c}\) by substituting in the initial condition for \(\vec{r}(0)\) at \(t = 0\). This gives \(\vec{c} = \vec{r}(0)\).
\[ \vec{r}(t) = \left[ \frac{1}{2}(5t^2+6) \hat{\imath} + 2(t^3+1) \hat{\jmath} + (3t+1) \hat{k} \right] \]
14.1.2 Work and angle
A force \(\vec{f} = (5\hat{\imath} + 7\hat{\jmath} + 9\hat{k}) \text{ N}\) displaces a second particle from the origin to position vector \(\vec{r} = (2\hat{\imath} + 2\hat{\jmath} + 2\hat{k}) \text{ m}\). Using the scalar product, calculate the work done on the particle by the force, \(W = \vec{f} \cdot \vec{r}\) and find the angle between \(\vec{f}\) and \(\vec{r}\).
\[ W = \vec{f} \cdot \vec{r} = 5 \times 2 + 7 \times 2 + 9 \times 2 = 42 \text{ J} \] \[ \vec{f} \cdot \vec{r} = |\vec{f}| |\vec{r}| \cos \theta \] \[ |\vec{f}| = \sqrt{5^2 + 7^2 + 9^2} = 12.45 \text{ N} \] \[ |\vec{r}| = \sqrt{2^2 + 2^2 + 2^2} = 3.46 \text{ m} \] \[ \cos \theta = \frac{\vec{f} \cdot \vec{r}}{|\vec{f}| |\vec{r}|} = \frac{42}{12.45 \times 3.46} = 0.9750 \] \[ \theta = 12.8^\circ \]
14.1.3 Constant force
The next few questions are conceptual, and aimed at testing your understanding of Newton’s laws. They are also multiple choice. We haven’t covered the third law yet, but have a go anyway, as you should be familiar with the ideas from school.
A student exerts a constant horizontal force on a large box, causing it to move across a horizontal floor at constant speed \(v_0\). The constant force applied by the student:
- Is greater than either the weight of the box or the total force which resists its motion.
- Has the same magnitude as the weight of the box.
- Is greater than the total force which resists the motion of the box.
- Has the same magnitude as the total force which resists the motion of the box.
- Is greater than the weight of the box.
D - no acceleration, so forces must be balanced.
14.1.4 Constant force \(\times 2\)
The same student doubles the constant horizontal force exerted. The box then moves:
- For a while at a constant speed, greater than the speed \(v_0\), then with a speed that increases thereafter.
- For a while with an increasing speed, then with a constant speed thereafter.
- With a continuously increasing speed.
- With a constant speed that is double the speed \(v_0\), in the previous question.
- With a constant speed that is greater than the speed \(v_0\), but not necessarily twice as great.
C - forces unbalanced, so box accelerates.
14.1.5 Truck towing
A large truck breaks down, and receives a push back into town by a small compact car.
While the car, pushing the truck, is speeding up to a cruising speed:
- The amount of force with which the car pushes on the truck is equal to that with which the truck pushes back on the car.
- The amount of force with which the car pushes on the truck is smaller than that with which the truck pushes back on the car.
- The amount of force with which the car pushes on the truck is greater than that with which the truck pushes back on the car.
- The car’s engine is running so that car pushes against the truck, but the truck’s engine is not running so that truck cannot push back against the car. The truck is pushed forward simply because it is in the way of the car.
- Neither the car nor the truck exerts any force on the other. The truck is pushed forward simply because it is in the way of the car.
A - by Newton’s third law, the car and truck push on each other with equal and opposite forces.
After the car reaches the constant cruising speed at which its driver wishes to push the truck:
- The amount of force with which the car pushes on the truck is smaller than that with which the truck pushes back on the car.
- The amount of force with which the car pushes on the truck is greater than that with which the truck pushes back on the car.
- The car’s engine is running so that car pushes against the truck, but the truck’s engine is not running so that truck cannot push back against the car. The truck is pushed forward simply because it is in the way of the car.
- The amount of force with which the car pushes on the truck is equal to that with which the truck pushes back on the car.
- Neither the car nor the truck exerts any force on the other. The truck is pushed forward simply because it is in the way of the car.
D - as above, although the forces are now lower, as we only need to overcome friction. Without friction there would be no forces acting, and we would only be considering Newton’s first law.
14.1.6 River swim
- A swimmer crosses a river by swimming perpendicular to the bank. The river is flowing uniformly at \(1 \text{ m s}^{-1}\). The swimmer swims at a steady \(1 \text{ m s}^{-1}\) relative to the water. What is the swimmer’s velocity relative to the frame of the bank, and whereabouts do they land on the other bank, if the river is \(100 \text{ m}\) wide? How long does the crossing take?
A sketch of the problem is shown in Figure 14.1.
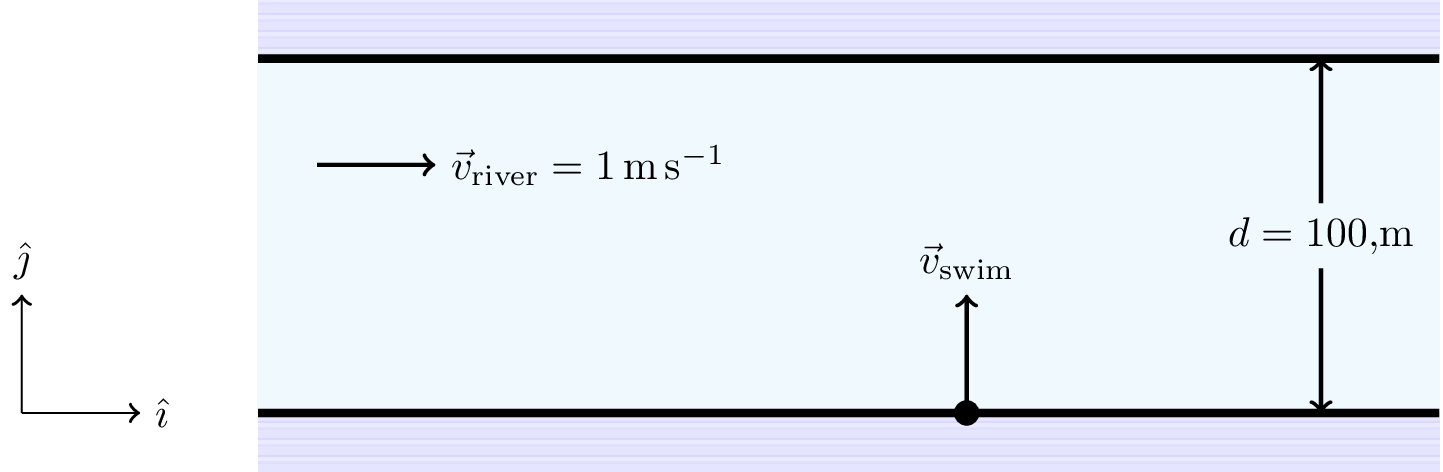
The velocity relative to the river bank is given by \[ \vec{v}_\text{bank} = \vec{v}_\text{swim} + \vec{v}_\text{river} \] as shown in Figure 14.2.
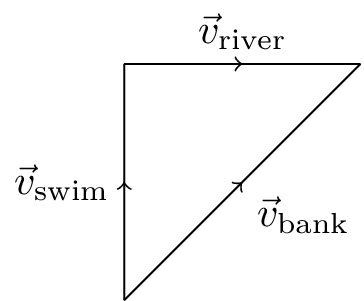
\[ \vec{v}_\text{bank} = \left| \vec{v}_\text{swim} \right| \hat{\imath} + \left| \vec{v}_\text{river} \right| \hat{\jmath} = (\hat{\imath} + \hat{\jmath}) \text{ m s}^{-1} \]
For the crossing time, consider the perpendicular component \[ d = \left| \vec{v}_\text{swim} \right| \times t \] \[ \implies t = \frac{100}{1} = 100 \text{ s} \]
Position vector of landing relative to starting point on the bank \(\vec{r}_\text{start} = (0,0)\) is given by \[ \vec{r}_\text{end} = \vec{v}_\text{bank} \times t = 100 (\hat{\imath} + \hat{\jmath}) \text{ m} \] You could also obtain this geometrically because the trajectory is \(45^\circ\) to the bank.
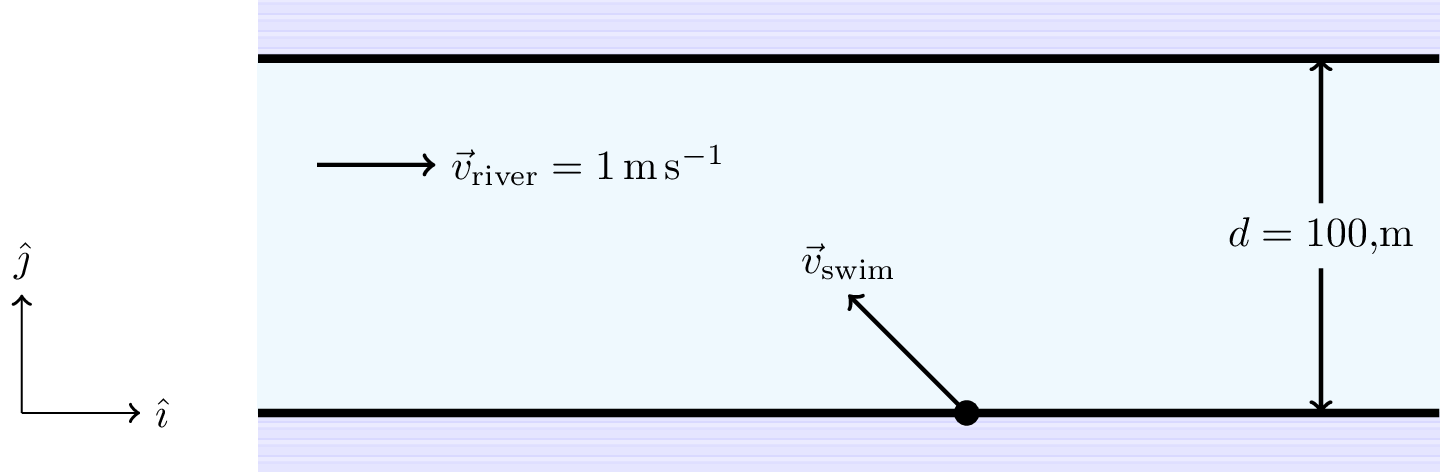
- The same swimmer attempts to cross the river again but, on this occasion, they aim to land directly opposite their starting position. In what direction should they swim, and how long will the crossing take, if they swim at \(2 \text{ m s}^{-1}\) relative to the water?
This is similar to before (see Figure 14.3), \[ \vec{v}_\text{bank} = \vec{v}_\text{swim} + \vec{v}_\text{river}, \] but now we want \(\vec{r}_\text{bank}\) parallel to \(\vec{\jmath}\) and \(\left| \vec{v}_\text{swim} \right| = 2 \text{ m s}^{-1}\).
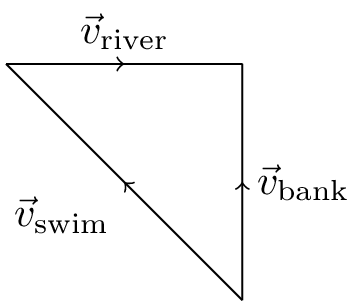
From Figure 14.4, we can see that \[ \left| \vec{v}_\text{swim} \right|^2 = \left| \vec{v}_\text{river} \right|^2 + \left| \vec{v}_\text{bank} \right|^2 \] \[ 4 = 1 + \left| \vec{v}_\text{bank} \right|^2 \] Substituting in the numbers gives \[ \vec{v}_\text{bank} = \sqrt{3} \hat{\jmath} \text{ m s}^{-1} \] and a crossing time of \[ t = \frac{100}{\sqrt{3}} = 57.7 \text{ s} \] The direction is given by \(\theta\), \[ \cos \theta = \frac{ \left| \vec{v}_\text{bank} \right|}{\left| \vec{v}_\text{swim} \right| |} = \frac{\sqrt{3}}{2} = 0.866 \] \[ \theta = 30^\circ \]
14.2 Part 2 – Problem-solving question
Summative (i.e., counts 3.75% towards final grade), please submit PDF as a group
The problem solving question will be provided during the workshop session.