4 Newton’s first law
As physicists we want to understand how the Universe works. We want to be able to quantitatively describe the motion of objects, and to explain and predict their behaviour. The foundation of classical mechanics is described by Newton’s laws.
Newton’s laws of motion describe how objects move in response to forces. They are the foundation of classical mechanics. They are well tested and found to be a good description of “every-day” physics.
There are three laws, and we will go through each in turn.
4.1 Newton’s first law and inertial reference frames
Why do objects start to move, change direction, or speed? Galileo and Newton realised that a force is required to change velocity. (Note that velocity is a vector so this includes a change in direction even if the speed remains constant). Newton found that the acceleration of an object is proportional to the force acting on it, i.e., \[ \vec{F} \propto \frac{d\vec{v}}{dt} \] where the constant of proportionality is the mass of the object giving (spoiler alert) Newton’s second law \[ \vec{F} = m\vec{a}, \] but more on this later…
Classical mechanics relates the motion of objects to the forces that act on them. These are described by Newton’s three laws of motion, and we shall go through each in turn.
An object at rest will remain at rest, and an object in motion will remain in motion at constant velocity, unless acted upon by an external force.
If no net force acts on an object, a reference frame in which the acceleration of the object remains zero is an inertial reference frame.
4.1.1 Galilean transformation
We can transform between two inertial reference frames using a Galilean transformation. Let’s consider a one dimensional example. Two frames, \(A\), and \(B\), are initially coincident. Frame \(B\) is moving relative to frame \(A\) with a velocity \(v\) in the \(x-\)direction. This means that at time \(t\) the origin of frame \(B\) is at \(x = vt\) when measured in frame \(A\).
We can write the position of an object \(P\) in frame \(B\) in two ways. In terms of the coordinate system in frame \(B\), the object is at a position \(x'\).
In terms of teh coordinate system in frame \(A\), the object is at position \[ x = vt + x' \] which is illustrated in Figure 4.1.
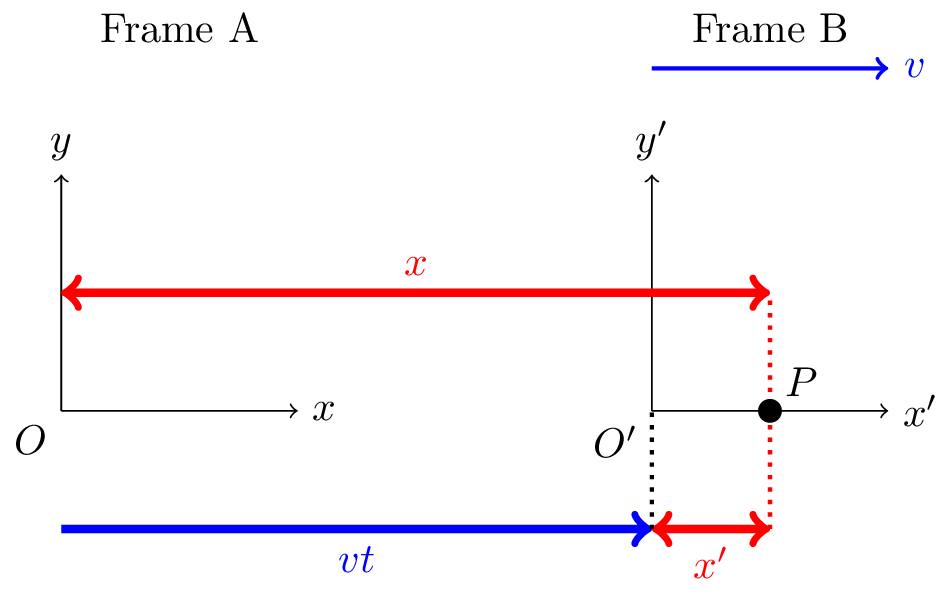
The velocity of \(P\) measured in frame \(A\) is obtained by differentiation \[ \frac{dx}{dt} = v + \frac{dx'}{dt} \] \[ u = v + u' \] where \(u\) is the velocity of \(P\) measured in frame \(A\) and \(u'\) is the velocity of \(P\) measured in frame \(B\).
The acceleration can be obtained by differentiating again \[ \frac{d^2x}{dt^2} = 0 + \frac{d^2x'}{dt^2} \] which is the same in both frames.
This also means that the forces are the same in both frames. The profound implication is that the laws of physics are the same in inertial frames! Furthermore, you can’t tell the speed by measuring force.
Transformations between frame \(A\) (unprimed coordinates) and \(B\) (primed coordinates) are as follows.
Displacement \(x\) in \(A\) and \(x'\) in \(B\). \[ x = vt + x' \]
Velocity \(u\) in \(A\) and \(u'\) in \(B\). \[ u = v + u' \] Acceleration \(a\) in \(A\) and \(a'\) in \(B\) are the same. \[ a = a' \] These can be generalised to three dimensions using vectors.
If an object is moving at a constant velocity in an inertial reference frame, which of the following can you deduce?
- No forces act on the object
- A constant force acts on the object in the direction of motion
- The net force acting on the object is zero
- The net force acting on the object is equal and opposite to its weight
- If there is any net force, the object will accelerate.
Galilean relativity does not always work. For example, what happens when velocities approach the speed of light? You’ll find out in the Special Relativity class next year (or you can read about it in the course textbook).
4.2 Conservation of momentum
Newton’s first law tells us that in the absence of external forces a system’s total momentum must be conserved. Momentum conservation is an expression of Newton’s first law, i.e., \[ \frac{d\vec{p}_\text{tot}}{dt} = \vec{0} \] where \(\vec{p}_\text{tot}\) is the total momentum of the system that is constant.
Consider a system made up of \(N\) particles with masses \(m_i\), positions \(\vec{r}_i\), and velocities \(\vec{v}_i\). The total momentum of the system is \[ \vec{p}_\text{tot} = \sum_{i = 1}^N \vec{p}_i = \sum_{i = 1}^N m_i \vec{v}_i = \frac{d}{dt} \left( \sum_{i = 1}^N m_i \vec{r}_i \right) \tag{4.1}\] where \(\vec{p}_i\) is the momentum of the \(i^\text{th}\) particle.
Using the principle of moments (from A-level) the Centre of Mass (c.o.m.) of the system is \[ \sum_{i = 1}^N m_i (\vec{r}_i - \vec{r}_\text{com}) = \vec{0} \tag{4.2}\] where \(\vec{r}_\text{com}\) is the position of the centre of mass. This means that the centre of mass is the point about which the moment of the system is zero. See Figure 4.2 for an illustration of the system.
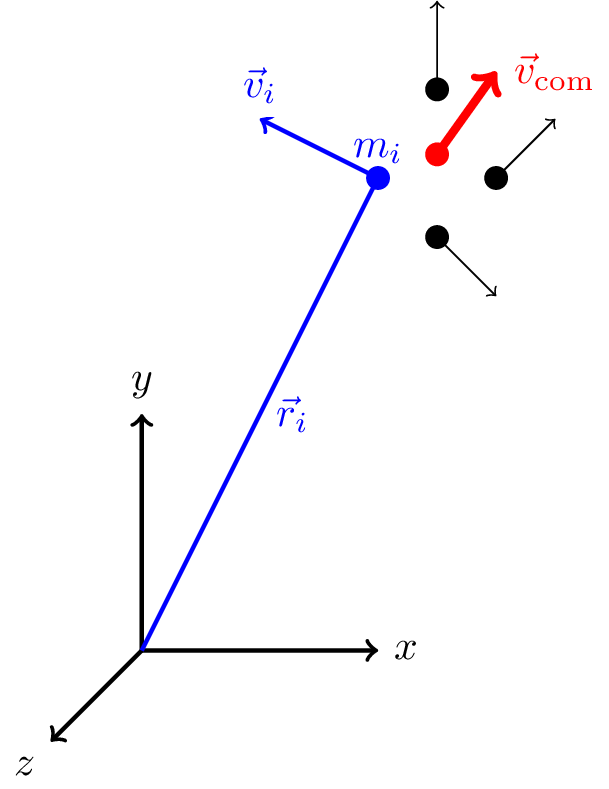
We can write the total mass \(M\) as the sum of the individual masses \[ M = \sum_{i = 1}^N m_i \] We can rearrange Equation 4.2 to get an expression for the centre of mass
\[ \vec{r}_\text{com} = \frac{1}{M} \sum_{i = 1}^N m_i \vec{r}_i \]
Then from Equation 4.1 we see that the total momentum \(\vec{p}_\text{tot}\) is \[ \vec{p}_\text{tot} = M \frac{d \vec{r}_\text{com}}{dt} = M \vec{v}_\text{com} \] where \(\vec{v}_\text{com}\) is the velocity of the centre of mass.
\[ \text{Total momentum} = \text{total mass} \times \text{velocity of centre of mass} \] It doesn’t matter what the individual particles are doing. We only need to think about the total mass and movement of the centre of mass.
For a system of particles we can identify the centre of mass and its net movement.
Under external forces the centre of mass behave like a point particle of mass \(M\) at \(\vec{r}_\text{com}\).
4.3 Centre of mass frame
The “centre of mass frame”, also known as the zero momentum frame, is an inertial frame moving at \(\vec{v}_\text{com}\) so that in this frame \(\vec{v}_\text{com}^\prime = \vec{0}\). This is the zero momentum frame.
An experiment of mass \(2m\) is launched from the origin at an angle \(\theta\) to the horizontal. In a previous identical test the projectile landed 55 m from the origin. However, in this test the experiment explodes at the highest point into into two pieces of equal mass. One piece has no horizontal motion, so falls directly downwards, landing at \(x_1\), while the other continues to move horizontally, landing at \(x_2\). This is illustrated in Figure 4.3. How far from the origin are \(x_1\), and \(x_2\)? You should neglect air resistance.
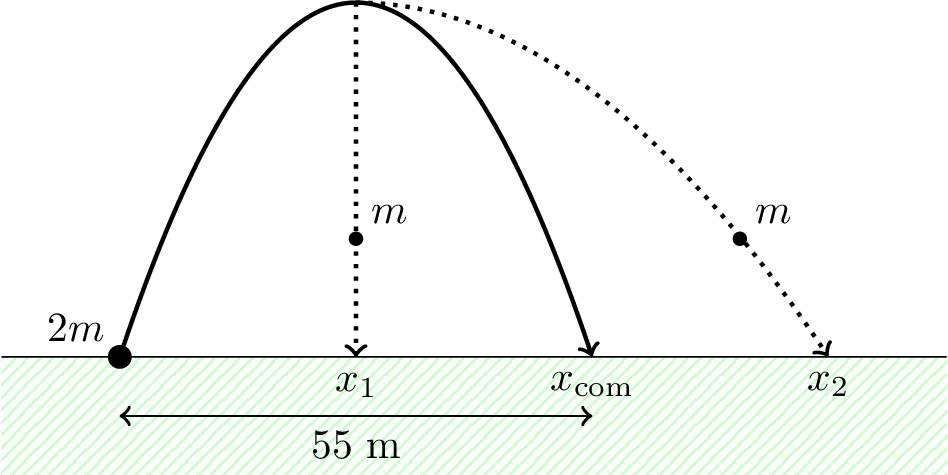
Neglecting air resistance means that the trajectory of the centre of mass is symmetric about the highest point. This means that the highest point is at \[x_1 = \frac{x_\text{com}}{2} = \frac{55}{2} = 27.5 \text{ m} \] where \(x_\text{com}\) is the centre of mass range shown in Figure 4.3.
Momentum is conserved when the experiment explodes, so the centre of mass will follow the same trajectory as it did in the first test flight when the experiment did not explode. We know from the definition of centre of mass that \[ (2m) x_\text{com} = m x_1 + m x_2 \] \[ 2 x_\text{com} = x_1 + x_2 \] We know \(x_\text{com}\) and \(x_1\), so we can calculate \[ x_2 = 110 - 27.5 = 82.5 \text{ m}. \]