11 Workshop 0
Week 1
This workshop is a reflection on A-level mechanics problems.
The purpose of the workshop is to get used to the workshop environment, get to know your course colleagues, discuss physics, and begin solving physics problems.
The problems are based on A-level mechanics. All problems are solvable using that knowledge. Discussions with colleagues and referring to notes, books and other resources are encouraged. You should bear in mind the following points:
- Solutions should be more than just strings of equations; there should be explanation and commentary to explain the solution.
- A diagram can help to answer questions; make sure your diagram is clear and large enough to label and write on. Diagrams can be too small – they are rarely too big!
11.1 Part 1 – Preliminary questions
Formative (i.e., not assessed), for practice, and answers do not need to be submitted
These are “primer” questions. The problems are based on A-level mechanics, and the solutions can be found using your mechanics notes. We will also cover this content later in the lectures, so don’t worry if you can’t remember everything now.
11.1.1 Force diagram
Draw force diagrams for a car in the following scenarios.
- Going uphill at constant velocity.
- Going downhill at constant velocity.
- Stationary on a hill.
This is an application of Newton’s first law. Since the car is either “at rest” or “moving at constant speed”, all forces are in balance. We also only consider “external forces”; i.e., we ignore “friction in wheel bearings”! For simplicity’s sake, we combine all “drag” forces.
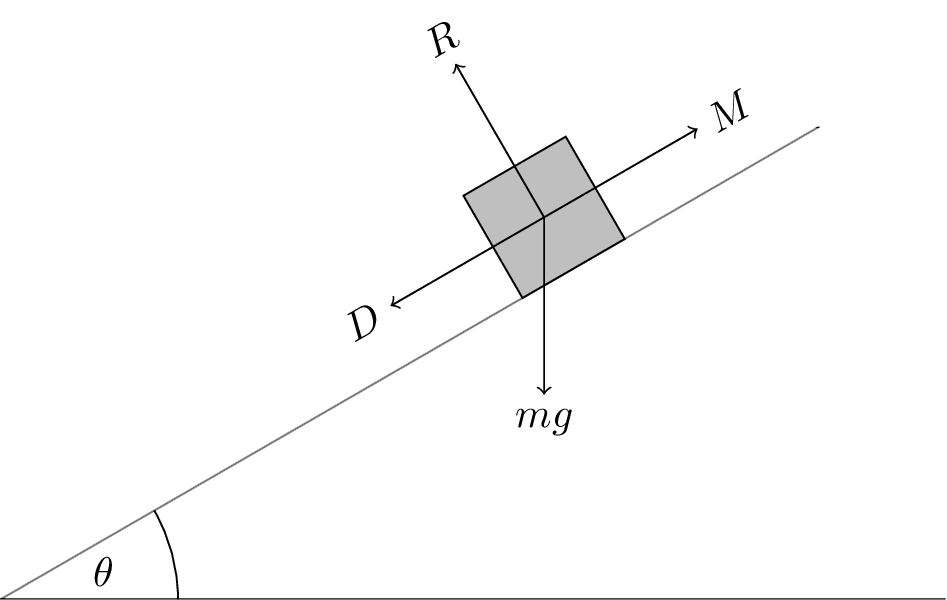
- Constant speed uphill.
- \(R = mg \cos \theta\) is the normal reaction force.
- \(M\) is the motive force.
- \(D\) is the drag force due to friction and air resistance.
- The motive force and drag force are balanced, \(M = D + mg \sin \theta\).
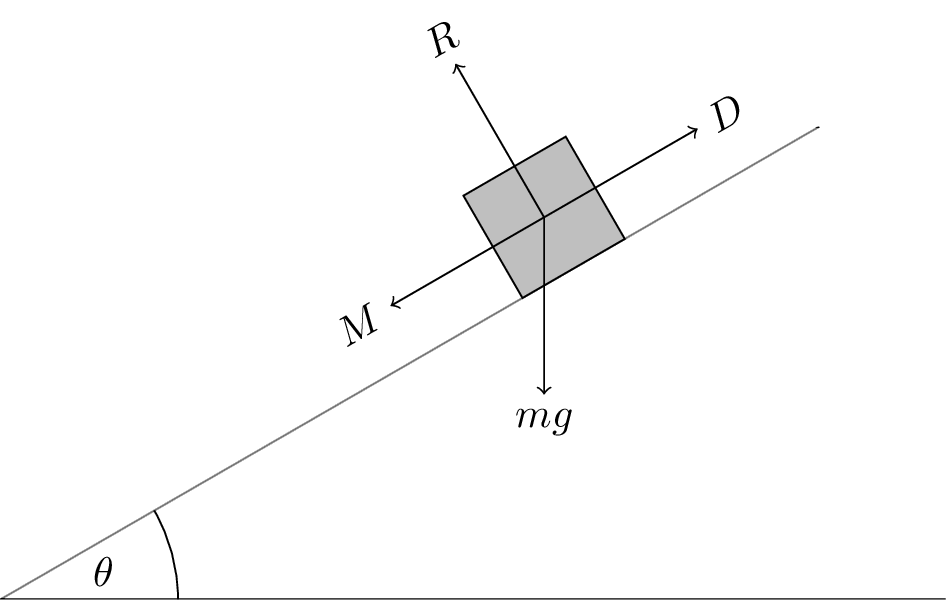
- Constant speed downhill.
- \(R = mg \cos \theta\) is the normal reaction force.
- \(M\) is the motive force (if needed).
- \(D\) is the drag force due to friction, air resistance, and braking (if needed).
- The motive force and drag force are balanced, \(D = mg \sin \theta + M\).
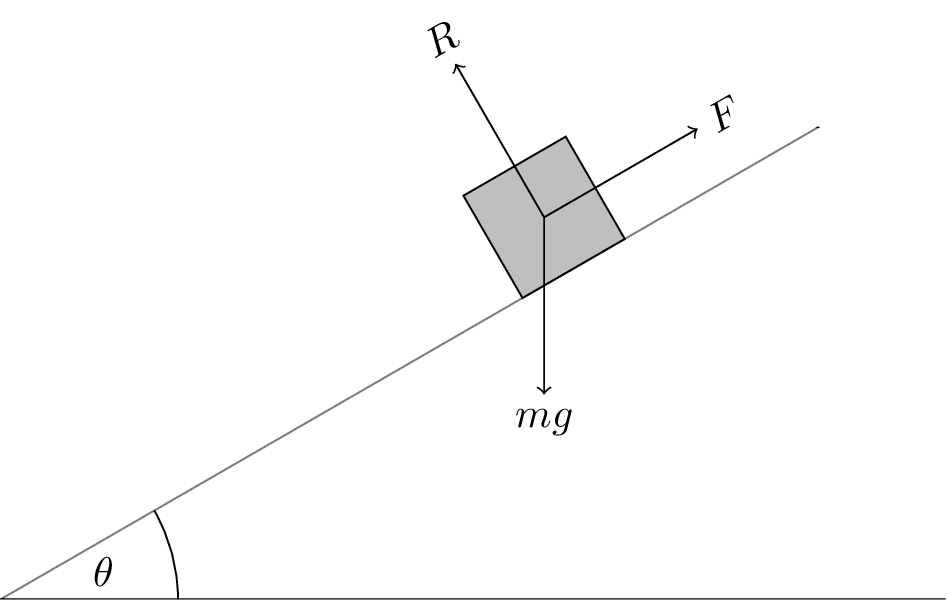
- Stationary car.
- \(R = mg \cos \theta\) is the normal reaction force.
- \(F\) is the friction force.
- The friction force and the component of gravitational force along the plane are balanced, \(F = mg \sin \theta\).
Note: These answers do contain some information that wasn’t asked for in the question, to help your understanding. We would only expect you to provide the information that is asked for in an exam!
11.1.2 Drone
A drone of mass \(1.0 \text{ kg}\) rises with constant acceleration from rest to a height of \(50 \text{ m}\) in \(10 \text{ s}\). Calculate the thrust (force) exerted by the rotors of the drone.
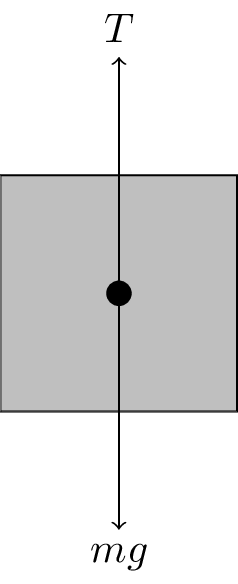
This is an application of Newton’s equations of motion to find the acceleration. Using \[ s = ut + \frac{1}{2} at^2 \] where the initial velocity \(u = 0 \text{ m s}^{-1}\) and rearranging to get \[ a = \frac{2s}{t^2}. \] We can then apply Newton’s second law, \(F = ma\). Looking at Figure 11.4, the net upward force providing the acceleration is \(F = T - mg\). \[ T - mg = ma \] \[ T = mg + ma \] \[ T = m\left(\frac{2s}{t^2} + g\right) \] Substituting in the numbers gives \[ T = 1 \times \left(\frac{2 \times 50}{10^2} + 9.8\right) = 11 \text{ N}. \]
11.1.3 Bicycle torque
A bicycle hub cassette must be tightened to a torque of \(50 \text{ Nm}\). If you have a spanner of length \(25 \text{ cm,}\) what is the perpendicular force required to obtain the correct torque?
To answer this question you need to recognise what a “moment” is. This is also an opportunity to mention dimensional analysis.

Torque, as illustrated in Figure 11.5, is \(\tau = Fd\). \[ F = \frac{\tau}{d} = \frac{50}{0.25} = 200 \text{ N}. \]
11.2 Part 2 – Problem-solving question
The problem solving question will be provided during the workshop session.
Full solution should be submitted as a single PDF as a group submission under “Assessment, Submission, and Feedback” link on Blackboard. One upload per group.