13 Cylindrical Coordinates
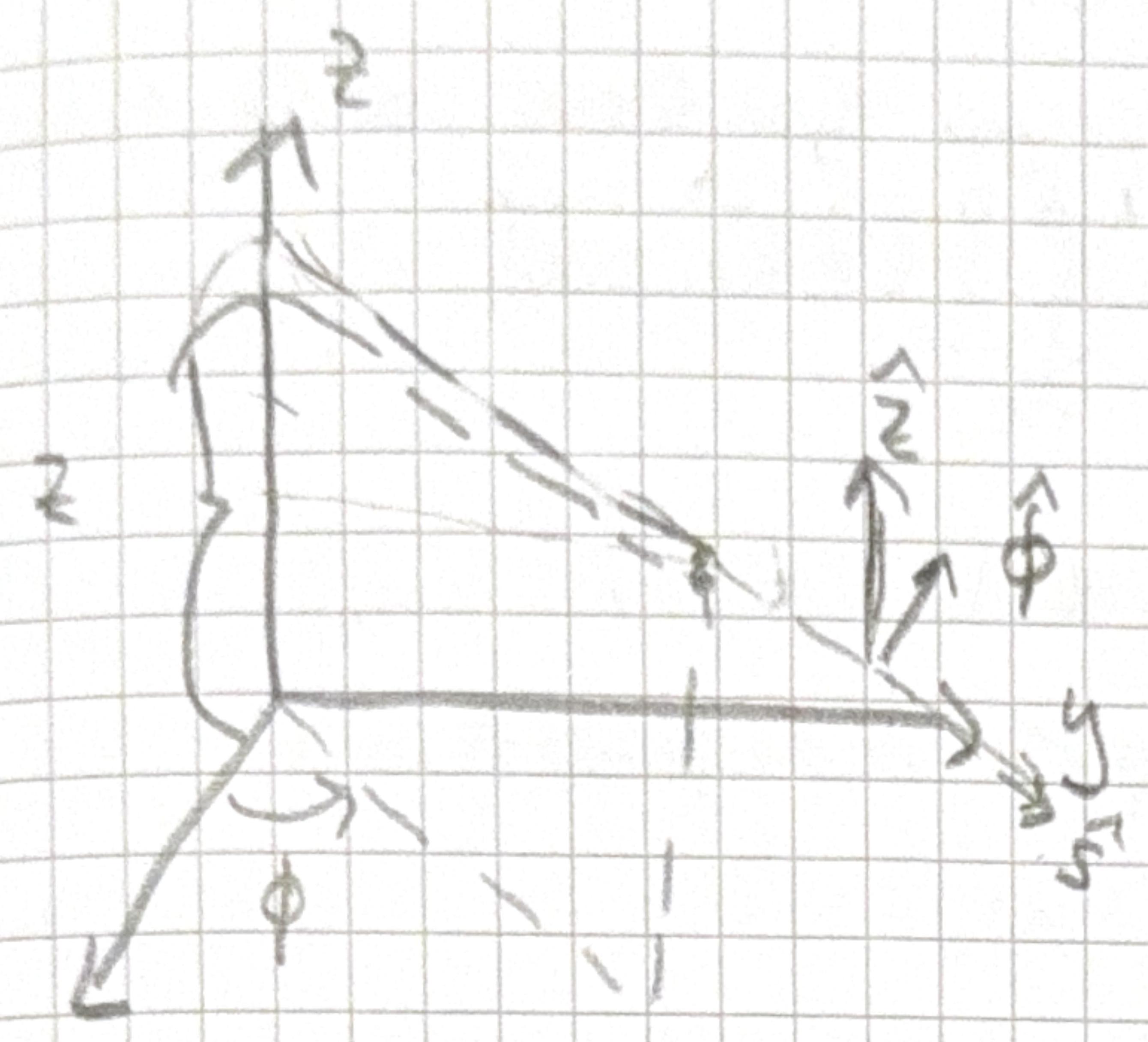
\(\phi\) - angle around \(x\)-axis ‘azimithal’ angle \(z\) - height in \(z\)-axis \(s\) - distance from \(z\)-axis
The relation to Cartesian coordinates
\[ \begin{aligned} & x=s \cos \phi \quad y=s \sin \phi \quad z=z \\ & \hat{s}=\cos \phi \hat{x}+\sin \phi \hat{y} \\ & \hat{\phi}=-\sin \phi \hat{x}+\cos \phi \hat{y} \\ & \hat{z}=\hat{z} \\ & d l_{s}=d s \quad d l_{\phi}=s d \phi \quad d l_{z}=d z \\ & d \mathbf{l}=d s \hat{s}+s d \phi \hat{\phi}+d z \hat{z} \end{aligned} \] volume element \(d \tau=s d s d \phi d z\). The range of \(s\) is 0 to \(\infty, \phi\) is 0 the \(2 \pi, z\) is \(-\infty\) to \(\infty\)
Vector operations in cylindrical coordinates (\(f=h=1 \quad g = s\)):
Gradient:
\[ \begin{aligned} \nabla t_{u}&=\frac{1}{f} \frac{\partial t}{\partial u}, \nabla t_{v}=\frac{1}{g} \frac{\partial t}{\partial v}, \nabla t_{w}=\frac{1}{h} \frac{\partial t}{\partial w} \\ \nabla t &= \frac{\partial t}{\partial s}\hat{s}+\frac{1}{s} \frac{\partial t}{\partial \phi} \hat{\phi}+\frac{\partial t}{\partial z}\hat{z} \end{aligned} \]
Divergence: \[ \begin{aligned} \nabla \cdot \mathbf{A} &= \frac{1}{fgh}\left[\frac{\partial}{\partial u}(gh A_u) + \frac{\partial}{\partial v} + (fh A_v)\frac{\partial}{\partial w}(fg A_w) \right]\\ \nabla \cdot \mathbf{v} &=\frac{1}{s} \frac{\partial}{\partial s}\left(s v_{s}\right)+\frac{1}{s} \frac{\partial v_\phi}{\partial \phi}+\frac{\partial v_z}{\partial z} \end{aligned} \]
Curl: \[ \begin{aligned} \nabla \times \mathbf{A} &= \frac{1}{g h}\left[\frac{\partial}{\partial v}\left(h A_{w}\right)-\frac{\partial}{\partial w}\left(gA_{v}\right)\right]\hat{u} \\ & +\frac{1}{f h}\left[\frac{\partial}{\partial w}(f A_u)-\frac{\partial}{\partial u}(h A_w)\right]\hat{v} \\ & +\frac{1}{f g}\left[\frac{\partial}{\partial u}(g A_v)-\frac{\partial}{\partial v}\left(f A_{u}\right)\right] \hat{w} \\ \nabla \times \mathbf{v} &= \left[ \frac{1}{s}\frac{\partial v_z}{\partial \phi} - \frac{\partial v_\phi}{\partial z}\right] \hat{s} + \left[\frac{\partial v_s}{\partial z} - \frac{\partial v_z}{\partial s}\right] \hat{\phi} \\ &+ \frac{1}{s}\left[\frac{\partial }{\partial s}(s v_\phi) - \frac{\partial v_s}{\partial \phi}\right] \hat{z} \end{aligned} \]
Laplacian: \[ \begin{aligned} \nabla^2 t &= \frac{1}{fgh}\left[\frac{\partial}{\partial u}\left(\frac{gh}{f}\right)\frac{\partial t}{\partial u} + \frac{\partial}{\partial v}\left(\frac{fh}{g}\right)\frac{\partial t}{\partial v} + \frac{\partial}{\partial w}\left(\frac{fg}{h}\right)\frac{\partial t}{\partial w}\right]\\ \nabla^2 t &= \frac{1}{s}\frac{\partial}{\partial s}\left(s \frac{\partial t}{\partial s}\right) + \frac{1}{s^2}\frac{\partial^2 t}{\partial \phi^2}+\frac{\partial^2 t}{\partial z^2} \end{aligned} \]
Find the divergence of the function \[ \begin{aligned} \mathbf{v} & =s\left(2+\sin ^{2} \phi\right) \hat{s}+s \sin \phi \cos \phi \hat{\phi}+3 z \hat{z} \end{aligned} \]
\[ \begin{aligned} \nabla \cdot \mathbf{v} &=\frac{1}{s} \frac{\partial}{\partial s}\left(s v_{s}\right)+\frac{1}{s} \frac{\partial v_\phi}{\partial \phi}+\frac{\partial v_z}{\partial z} \\ & =\frac{1}{s} \frac{\partial}{\partial s}\left[s\left(2 s+s \sin ^{2} \phi\right)\right]+\frac{1}{s} \frac{\partial}{\partial \phi} (s \sin \phi \cos \phi)+\frac{\partial}{\partial z} 3 z \\ & =\frac{1}{s} \frac{\partial}{\partial s}\left(2 s^{2}+s^{2} \sin ^{2} \phi\right)+\frac{1}{s} \cdot s \frac{\partial}{\partial \phi}(\sin \phi \cos \phi)+3 \\ & =\frac{2}{s} \cdot 2 s+2 s \sin ^{2} \phi+\cos \phi \cos \phi-\sin \phi \sin \phi+3 \\ & =4+2 \sin ^{2} \phi+\cos ^{2} \phi-\sin ^{2} \phi+3 \\ & =7+\sin ^{2} \phi+\cos ^{2} \phi=8 . \end{aligned} \]
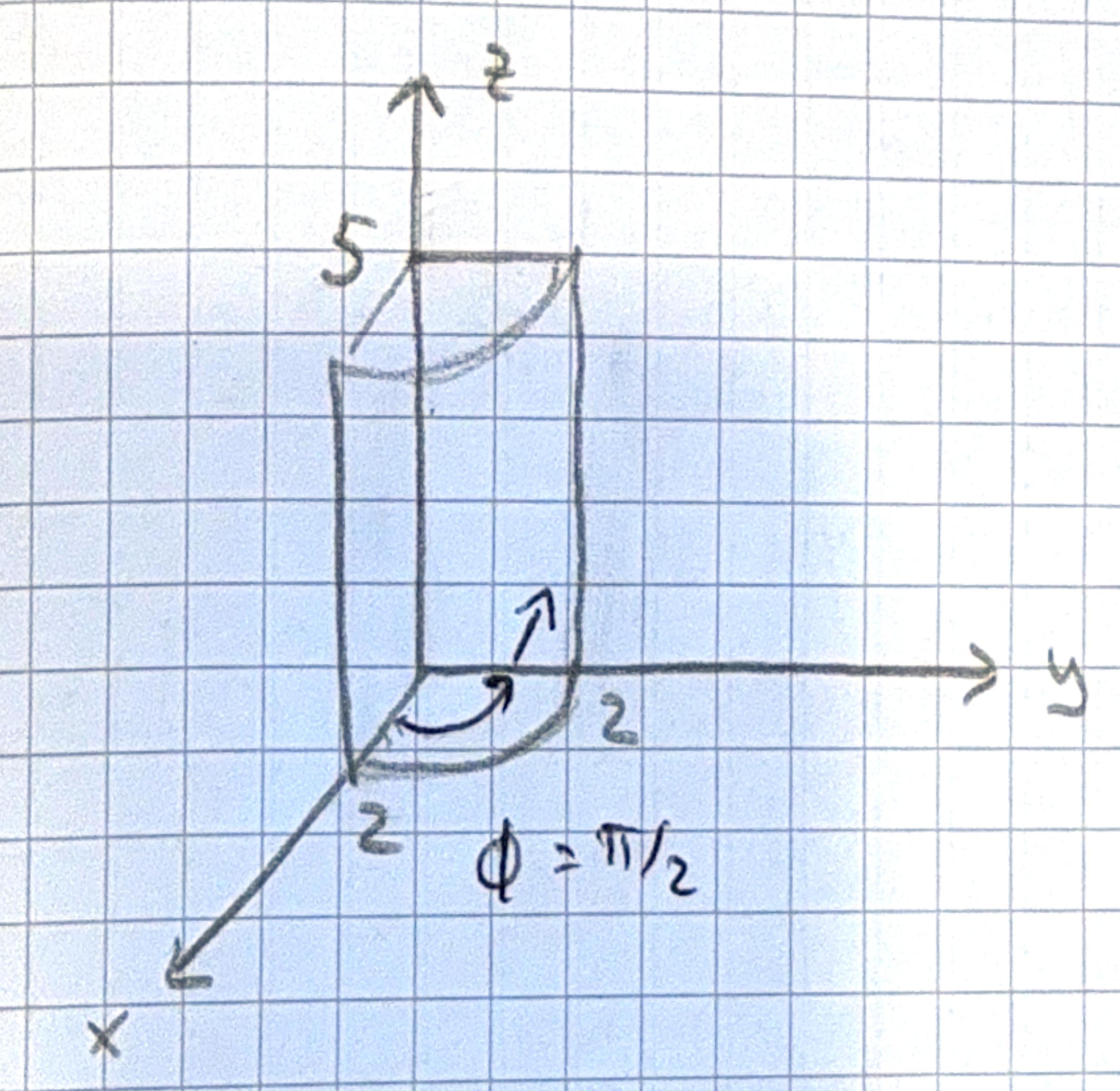
Test the divergence theorem for this function using a quarter-cylinder \((r=2, h=5)\).
 \[
\int_{V}(\nabla \cdot \mathbf{v}) d \tau=\oint_{S} \mathbf{v} \cdot d \mathbf{a}
\]
\[
\int_{V}(\nabla \cdot \mathbf{v}) d \tau=\oint_{S} \mathbf{v} \cdot d \mathbf{a}
\]
Left side - we have already calculated the div \[ \begin{aligned} & d \tau=s \, d s d \phi d z \\ & \int 8 s\, d s d \phi d z=\int_{0}^{5} \int_{0}^{\pi / 2} \int_{0}^{2} 8 s\, d s d \phi d z \end{aligned} \]
All constants so can be split up \[ \begin{aligned} \int_{v}(\nabla \cdot \mathbf{v})\, d \tau & =8 \int_{0}^{5} d z \int_{0}^{\pi / 2} d \phi \int_{0}^{2} s d s \\ & =8\left(\left.\left.\left.z\right|_{0} ^{5} \cdot \phi\right|_{0} ^{\pi / 2} \frac{s^{2}}{2}\right|_{0} ^{2}\right) \\ & =8(5 \cdot \pi / 2 \cdot 2) \\ \int(\nabla \cdot \mathbf{v}) d \tau & =40 \pi \end{aligned} \]
Right hand side \[ \begin{aligned} \oint_{S} \mathbf{v} \cdot d \mathbf{a}= & \int_{top} \mathbf{v} \cdot d \mathbf{a}+\int_{bottom} \mathbf{v} \cdot d \mathbf{a}+\int_{front} \mathbf{v} \cdot d \mathbf{a}+\int_{back} \mathbf{v} \cdot d \mathbf{a} \\ & +\int_{left} \mathbf{v} \cdot d \mathbf{a} \end{aligned} \]
Top: \[ \begin{aligned} & d_\mathbf{a}=s d \phi d s \hat{z}, z=5 \\ & \begin{aligned} \mathbf{v} \cdot d \mathbf{a} & =3 z \cdot s d \phi d s=15 s d \phi d s \\ \int_{0}^{2} \int_{0}^{\pi / 2} 15 s s d \phi d s & =\pi /\left.2 \cdot \frac{15 s^{2}}{2}\right|_{0} ^{2} \\ & =15 \pi \end{aligned} \end{aligned} \]
Bottom: \[ \begin{aligned} & d \mathbf{a}=-s d \phi d s \hat{z}, z=0 \\ & \iint 0 d \phi d s=0 . \end{aligned} \]
Back: \[ \begin{aligned} & d a=d z d s \hat{\phi}, \phi=\pi / 2 \\ & \mathbf{v} \cdot d \mathbf{a}=s \sin \phi \cos \phi d s d z \\ & \int_{0}^{s} \int_{0}^{2} s \sin \phi \cos \phi d s d z=0 . \end{aligned} \]
Left: \[ \begin{aligned} & d \mathbf{a}=-d s d z \hat{\phi} \quad \phi=0 \\ & \int_{0}^{5} \int_{0}^{2} s \sin \phi \cos \phi d s d z=0 \end{aligned} \]
Front: \[ \begin{aligned} & d \mathbf{a}=s d \phi d z \hat{s} \quad s=2 \\ & \mathbf{v} \cdot d \mathbf{a}=s^{2}\left(z+\sin ^{2} \phi\right) d \phi d z \\ & \begin{aligned} \int \mathbf{v} \cdot d \mathbf{a} & =\int_{0}^{5} \int_{0}^{\pi / 2} s^{2}\left(2+\sin ^{2} \phi\right) d \phi d z \\ & =\int_{0}^{5} d z \int_{0}^{\pi / 2} 4\left(2+\sin ^{2} \phi\right) d \phi \\ & =5 \cdot 5 \pi=25 \pi \\ \text { Total } & =40 \pi \end{aligned} \end{aligned} \]