9 Multiple Integrals
9.1 Double Integrals
\(\int_{a}^{b} y d x=\int_{a}^{b} f(x) d x \Rightarrow\) area “under the curve” 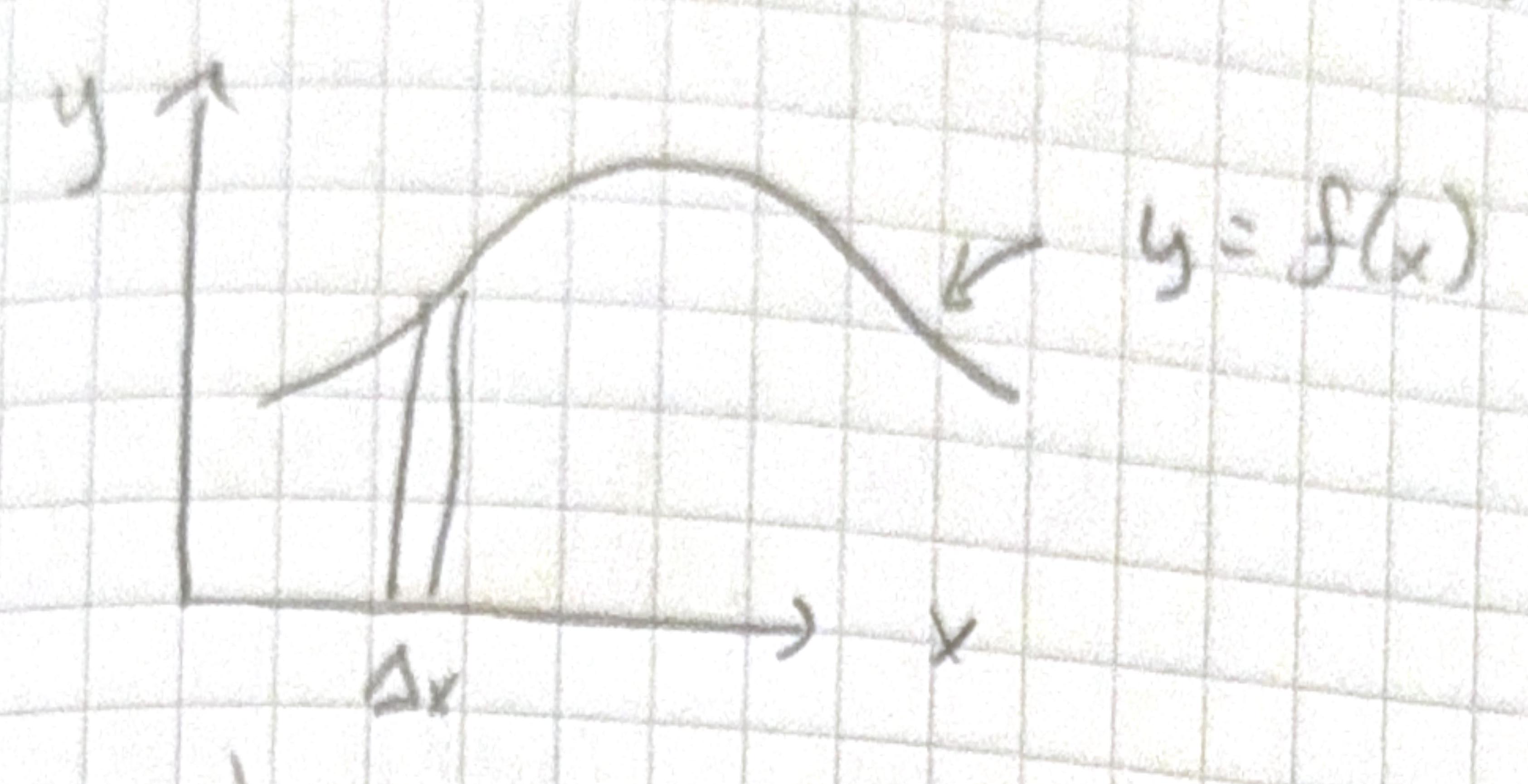
Define \(\int_{a}^{b} f(x) d x\) as the limit of the sum of the areas of rectangles.
What about three dimensional regions?
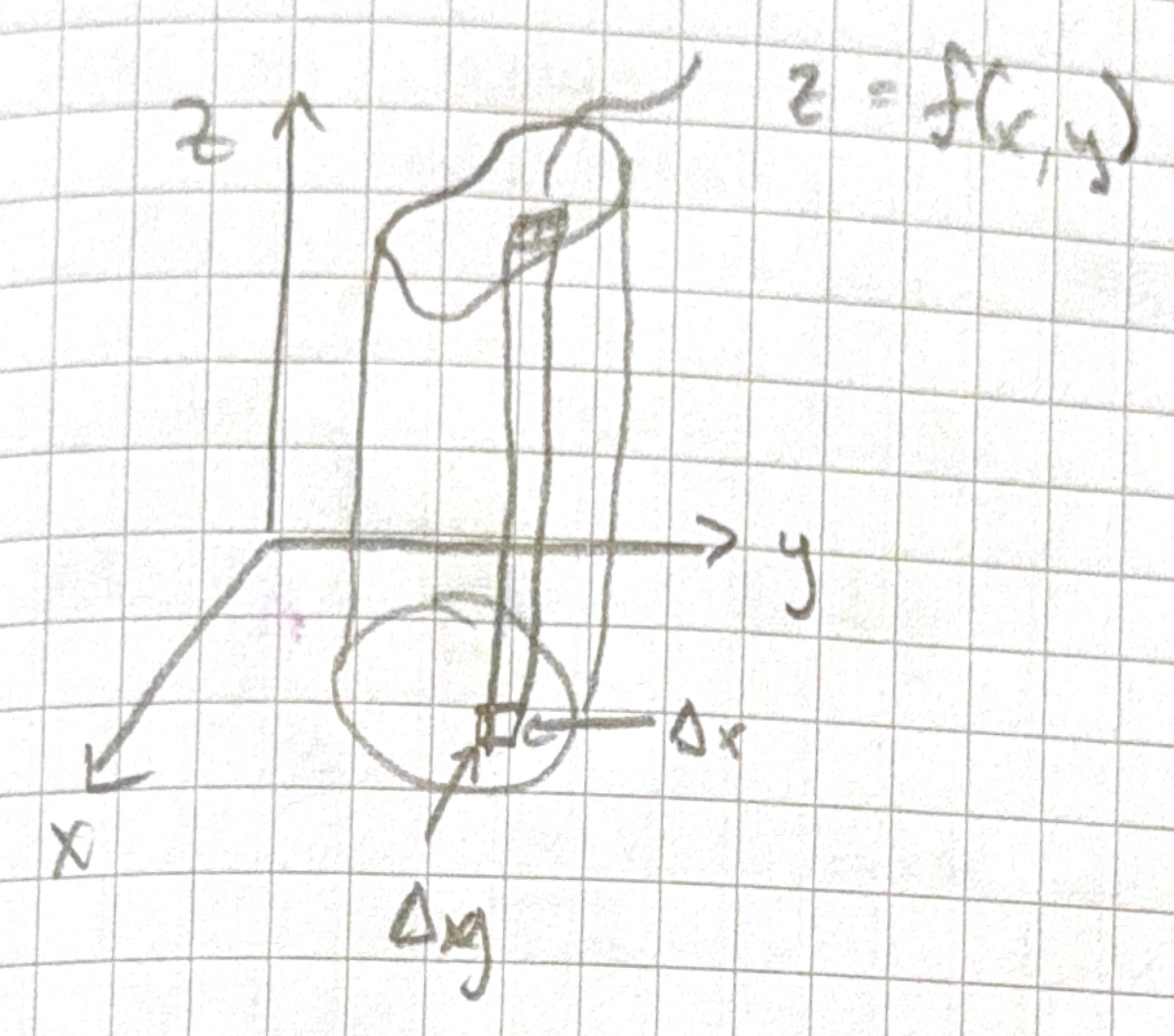
Create columns and add them up to find the volume. The column shown above has a cross section of \(\Delta A=\Delta x \Delta y\).
Find volume of the solid bounded by the coordinate planes (\(xz\), \(yz\), \(xy\)) and the planes \(z=1+y\) and \(-2 x+y=2\). (Example from Boas book - section on multiple integrals)
volume is integration (adding up) columns of height \(z\) and cros-sectional area \(\Delta A = \Delta x \Delta y\) \[ \begin{aligned} & V = \iint z d x d y=\iint(1+y) d x d y \end{aligned} \] Now decide which way to integrate first - integrate over y first holding x constant or integrate over x first and hold y constant (we could do either). I have chosen the former - in the xy plane build up a slice at a specific x value. So integrage over y first creating a slice of thickness dx. Now we need the limits for y. We start at y=0 and then reach the line y=2x+2. The value of the max y depends on the x value so the upper limit must be in terms of x. \[ \begin{aligned} & V = \int_{x=0}^{x= 1}\int_{y=0}^{y=2x+2}(1+y) d y d x \\ & =\int_{x=0}^{x= 1}\left(y+\left.\frac{y^{2}}{2}\right|_{0} ^{2-2 x}\right) dx\\ & =\int_{0}^{1} 2-2 x+\frac{(2-2 x)^{2}}{2} dx \\ & =\int_0^1 2-2 x+\frac{4-8 x+4 x^{2}}{2} dx\\ &=\int_0^1 4 -6 x+ 2 x^{2} dx\\ & = 4 x-3 x^{2}+\left.\frac{2}{3} x^{3}\right|_{0} ^{1} \\ & = 4-3+\frac{2}{3}=\frac{5}{3} \end{aligned} \] Alternatively we could have added up the columns into slices keeping \(y\) constant and we would have gotten the same answer.
\[ \begin{gathered} \int_{y=0}^{y=2} \int_{x=0}^{x = 2-y / 2}(1+y) d x dy\\ \left.\int_{0}^{2}(1+y) x\right|_{x=0} ^{x=1-y / 2} dy\\ \int_{0}^{2}(1+y) \cdot(1-y / 2) d y \\ \int_{0}^{2} 1-\frac{y}{2}+y-\frac{y^2}{2} d y \\ \int_{0}^{2} 1+\frac{y}{2}-\frac{y^{2}}{2} d y \\ 2+\frac{y^{2}}{4}-\left.\frac{y^{3}}{6}\right|_{0} ^{2} \\ 3-\frac{4}{3}=\frac{5}{3} \end{gathered} \]
The volume calculation above is an example of an iterated integral - holding a variable constant calculating one integral (inner most) then integrating over the variable that you just held constant. We did that example in both options x then y and y then x but often one way is easier than the other.
In the special case of rectangle (both \(x\) and \(y\) are constant) \[ f(x, y)=g(x) h(y) \] then \(\int_{x=1}^{b} \int_{y=c}^{d} g(x) h(y) d y d x\) \[ \left(\int_{0}^{b} g(x) d x\right)\left(\int_{c}^{d} h(y) d y\right) \]
Can use double integral to find more than just volume.
Find mass of rectangular plate bounded by \(x+0, x=2 \quad y=0, y = 1\) if its density (mass/area), is \(f(x, y)=xy\).
\[ \begin{aligned} & \Delta A = \Delta x A \Delta y \\ & \Delta M = f(x, y) \Delta x \Delta y\\ & M=\iint_{A} f(x, y) d x d y \\ & \int_{y=0}^{y=2} \int_{x=0}^{x=1} x y d x d y \\ & \int_{0}^{1} y d y \int_{0}^{2} x d x \\ & \left.\left.\frac{y^{2}}{2}\right|_{0} ^{1} \cdot \frac{x^{2}}{2}\right|_{0} ^{2}=1 \end{aligned} \]
9.2 Triple Integrals
We could have used a triple integral in the first problem - to create the column in the \(z\) direction.
Find \(V\) of solid in previous problem using a triple integral.
\[ \begin{aligned} & V = \iiint d x d y d z \end{aligned} \] Now figure out order - we want to create column in z first so integrate in z first holding both x and y constant then lets hold x constant and integrate over y.
\[ \begin{aligned} & V = \iiint d x d y d z \\ = & \int_{0}^{1}\left(\int_{0}^{2-2 x} \left[\int_{0}^{1+y} d z\right] d y\right) d z \\ = & \int_{x=0}^{1} \int_{y=0}^{2 - 2 x}(1+y) d y d x =5 / 3 \end{aligned} \]