15  Problems

15.1 Week 2

Question
  1. Find the gradients of: \[ \begin{aligned} &f(x, y, z) = x^2 + y^3 + z^4 \\ &f(x, y, z) = x^2y^3z^4\\ &f(x, y, z) = e^x \sin (y)\, ln (z) \end{aligned} \]

\[ \begin{aligned} &2x\hat{x} + 3y^2\hat{y} + 4z^3\hat{z}\\ &2xy^3z^4\hat{x} + 3x^2y^2z^4\hat{y} + 4x^2y^3z^3\hat{z}\\ &e^x \sin (y)\, ln(z) \hat{x} + e^x \cos (y)\, ln(z) \hat{y}+ \frac{e^x \sin (y)}{z} \hat{z} \end{aligned} \]

Question
  1. The height of a hill (in feet) is given by the function: \(h(x,y) = 10(2xy - 3x^2 - 4y^2 - 18x +28y +12)\) where \(y\) is the distance (in miles) north, \(x\) is the distance east of the town of Trout.

  1. Where is the top of the hill located?

  2. How high is the hill?

  3. How steep is the slope (in feet per mile) at a point one mile north and one mile east of Trout? In what direction is the slope steepest, at that point?

Part (a) \[ \begin{aligned} \nabla h &= 0 \quad \text{at summit} \\ \nabla h &= 10(2y-6x-18)\hat{x} + 10(2x-8y+28)\hat{y} \end{aligned} \]

Both \(\hat{x}\) component and the \(\hat{y}\) component are equal to \(0\) at the summit.

\[ \begin{aligned} \text{x component: } &2y - 6x -18 = 0 \\ \text{y component: } &2x-8y+28 = 0\\ &y = 3 \quad x = -2\\ &\text{three miles north, two miles west of Trout.} \end{aligned} \]

Part (b)

\[ h(-2,3) = 720 \text{ ft} \]

Part (c)

\[ \begin{aligned} &\nabla h (1,1) = -220 \hat{x} + 220 \hat{y}\\ &\left|\nabla h \right| = 220 \sqrt{2} \text{ northwest} \end{aligned} \]

Question
  1. Calculate the divergence of the following vector functions:

\[ \begin{aligned} \mathbf{v_a} &=& x^2 \hat x + 3xz^2 \hat y - 2xz \hat z \\ \mathbf{v_b} &=& xy \hat x + 2 yz \hat y + 3 z x \hat z\\ \mathbf{v_c} &=& y^2 \hat x + (2xy +z^2) \hat y + 2yz \hat z \end{aligned} \]

\[ \begin{aligned} \nabla \cdot \mathbf{v_a} &= \left ( \frac{\partial}{\partial x} \hat{x} + \frac{\partial}{\partial y} \hat{y} +\frac{\partial}{\partial z} \hat{z} \right ) \cdot (x^2 \hat{x} + 3xz \hat{y} -2xz\hat{z})\\ &= 2x - 2x\\ &= 0. \\ \\ \nabla \cdot \mathbf{v_b} &= y + 2z +3x\\ \\ \nabla \cdot \mathbf{v_c} &= 2x + 2y \end{aligned} \]

Question
  1. Calculate the curls of the vector functions in problem 3.

\[ \begin{aligned} & \underline{v}_{a}=x^{2} \hat{x}+3 x z^{2} \hat{y}-2 x z \hat{z} \\ & \nabla \times \underline{v}_a=\left|\begin{array}{ccc} \hat{x} & \hat{y} & \hat{z} \\ \partial / \partial x & \partial / \partial y & \partial / \partial z \\ x^{2} & 3 x z^{2} & -2 x z \end{array}\right| \\ & =\hat{x}\left(\partial / \partial y(-2 x z)-\partial /\partial z\left(3 x z^{2}\right)\right) \\ & -\hat{y}\left(\partial/ \partial x(-2 x z)-\partial / \partial z\left(x^{2}\right)\right) \\ & +\hat{z}\left(\partial / \partial x\left(3 x z^{2}\right)-\partial / \partial y\left(x^{2}\right)\right) \\ & =\hat{x}(-6 xz)-\hat{y}(-2 z)+\hat{z}\left(3 z^{2}\right) \\ & =-6 x \hat{x}+2 z \hat{y}+3 z^{2} \hat{z} \\ \\ & \underline{v}_{b}=x y \hat{x}+2 y z \hat{y}+3 z x \hat{z} \\ & \nabla \times \underline{v}_{b}=\left|\begin{array}{ccc} \hat{x} & \hat{y} & \hat{z} \\ \partial / \partial x & \partial / \partial y & \partial / \partial z \\ x y & 2 y z & 3 z x \end{array}\right| \\ & =\hat{x}(\partial / \partial y(3 z x)-\partial / \partial z(2 y z)) \\ & -\hat{y}(\partial / \partial x(3 z x)-\partial / \partial z(x y)) \\ & +\hat{z}(\partial / \partial x(z y z)-\partial / \partial y(x y)) \\ & =\hat{x}(-2 y)-\hat{y}(3 z)+\hat{z}(-x) \\ & =-2 y \hat{x}-3 z \hat{y}-x \hat{z} \end{aligned} \] \[ \begin{aligned} \underline{v}_{c}=y^{2} \hat{x} & +\left(2 x y+z^{2}\right) \hat{y}+2 y z \hat{z} \\ \nabla \times \underline{v}_{c}= & \left|\begin{array}{ccc} \hat{x} & \hat{y} & \hat{z} \\ \partial / \partial x & \partial / \partial y & \partial / \partial z \\ y^{2} & 2 x y+z^{2} & 2 y^{z} \end{array}\right| \\ = & \hat{x}\left(\partial / \partial y(2 y z)-\partial / \partial z\left(2 x y+z^{2}\right)\right) \\ & -\hat{y}\left(\partial / \partial x(2 y z)-\partial / \partial z\left(y^{2}\right)\right) \\ & +\hat{z}\left(\partial / \partial x\left(2 x y+z^{2}\right)-\partial / \partial y\left(y^{2}\right)\right) \\ = & (2 z-2 z) \hat{x}-0 \hat{y}+(2 y-2 y) \hat{z} \\ = & \underline{0} \end{aligned} \]

Question
  1. Calculate the line integral of the function \(\mathbf{v} = x^2 \hat x + 2yz \hat y + y^2 \hat z\) from the origin to the point (1,1,1) by three different routes:
  1. \((0,0,0) \rightarrow (1, 0, 0) \rightarrow (1, 1, 0) \rightarrow (1,1,1)\)
  2. \((0,0,0) \rightarrow (0, 0, 1) \rightarrow (0, 1, 1) \rightarrow (1,1,1)\)
  3. the straight line.
  4. What is the line integral around the closed loop that goes out along path (a) and back along path (b)?

\[ \begin{aligned} & \underline{v}=x^{2} \hat{x}+2 y z \hat{y}+y^{2} \hat{z} \\ & \int_{P} \underline{v} \cdot d \underline{l} \\ & d \underline{\ell}=d x \hat{x}+d y \hat{y}+d z \hat{z} \end{aligned} \] a) three sections of path to integrate: \((0,0,0) \rightarrow(1,0,0) \rightarrow((, 1,0) \rightarrow\) \((1,1,1)\)

Part i: \(d \underline{l}=d x \hat{x} \quad y=0, z=0\) \[ \begin{aligned} \int_{\text {path }} x^{2} \hat{x} \cdot d x \hat{x} & =\int_{0}^{1} x^{2} d x \\ & =\left.\frac{x^{3}}{3}\right|_{0} ^{1}=\frac{1}{3} . \end{aligned} \]

Part ii: \(\quad d \underline{l}=d y \hat{y} \quad x=1, z=0\) \[ \begin{aligned} \int_{\text {path ii }} 2 y z \hat{y} \cdot d y \hat{y} & =\int_{0}^{1} 2 y z d y \\ & =0 \end{aligned} \] \[ \begin{aligned} & \text { Part iii: } d \underline{l}=d z \hat{z} \quad x=1, \quad y=1 \\ & \int_{\text {path } i i i} y^{2} \hat{z} \cdot d z \hat{z}=\int_{0}^{1} y^{2} d z=\int_{0}^{1} d z \\ & \text { Total path }=\int_{p} \underline{v} \cdot d \underline{l}=4 / 3 \end{aligned} \] b) Path \((0,0,0) \rightarrow(0,0,1) \rightarrow(0,1,1) \rightarrow(1,1,1)\) \[ \begin{aligned} & \text { Path i } y=0, x=0 \quad d \underline{\ell}=d z \hat{z} \\ & \int_{\text {Path }} y^{2} \hat{z} \cdot d z \hat{z}=\int_{0}^{1} 0 d z=0 \end{aligned} \] path_ii \(z=1, x=0 \quad d \underline{\ell}=d y \hat{y}\) \[ \begin{aligned} \int_{\text {path ii }} 2 y z \hat{y} \cdot d y \hat{y}=\int_{0}^{1} 2 y d y & =\left.y^{2}\right|_{0} ^{1} \\ & =1 \end{aligned} \]

Path iii: \(z=1, y=1 \quad d l=d x \hat{x}\) \[ \begin{aligned} \int_{\text {path iii }} x^{2} \hat{x} \cdot d x \hat{x}=\int_{0}^{1} x^{2} d x & =\left.\frac{x^{3}}{3}\right|_{0} ^{1} \\ & =\frac{1}{3} \end{aligned} \] \[ \text { Total path }=\int_{p} \underline{v} \cdot d \underline{l}=4 / 3 \text {. } \]

  1. \[ \begin{aligned} & x=y=z \quad, \quad d x=d y=d z \\ &\int_{p} \underline{v} \cdot d \underline{\ell} \\ & =\int\left(x^{2} \hat{x}+2 y z \hat{y}+y^{2} \hat{z}\right) \cdot(d x \hat{x}+d y \hat{y}+d z \hat{z}) \\ & =\int x^{2} d x+2 y z d y+y^{2} d z \end{aligned} \] now write all in terms of one variable. \[ \begin{aligned} & =\int x^{2} d x+2 x^{2} d x+x^{2} d x \\ & =\int_{0}^{1} 4 x^{2} d x \\ & =\left.\frac{4}{3} x^{3}\right|_{0} ^{1}=\frac{4}{3} \end{aligned} \]
  2. \(\oint v \cdot d l=4 / 3-4 / 3=0\).
Question
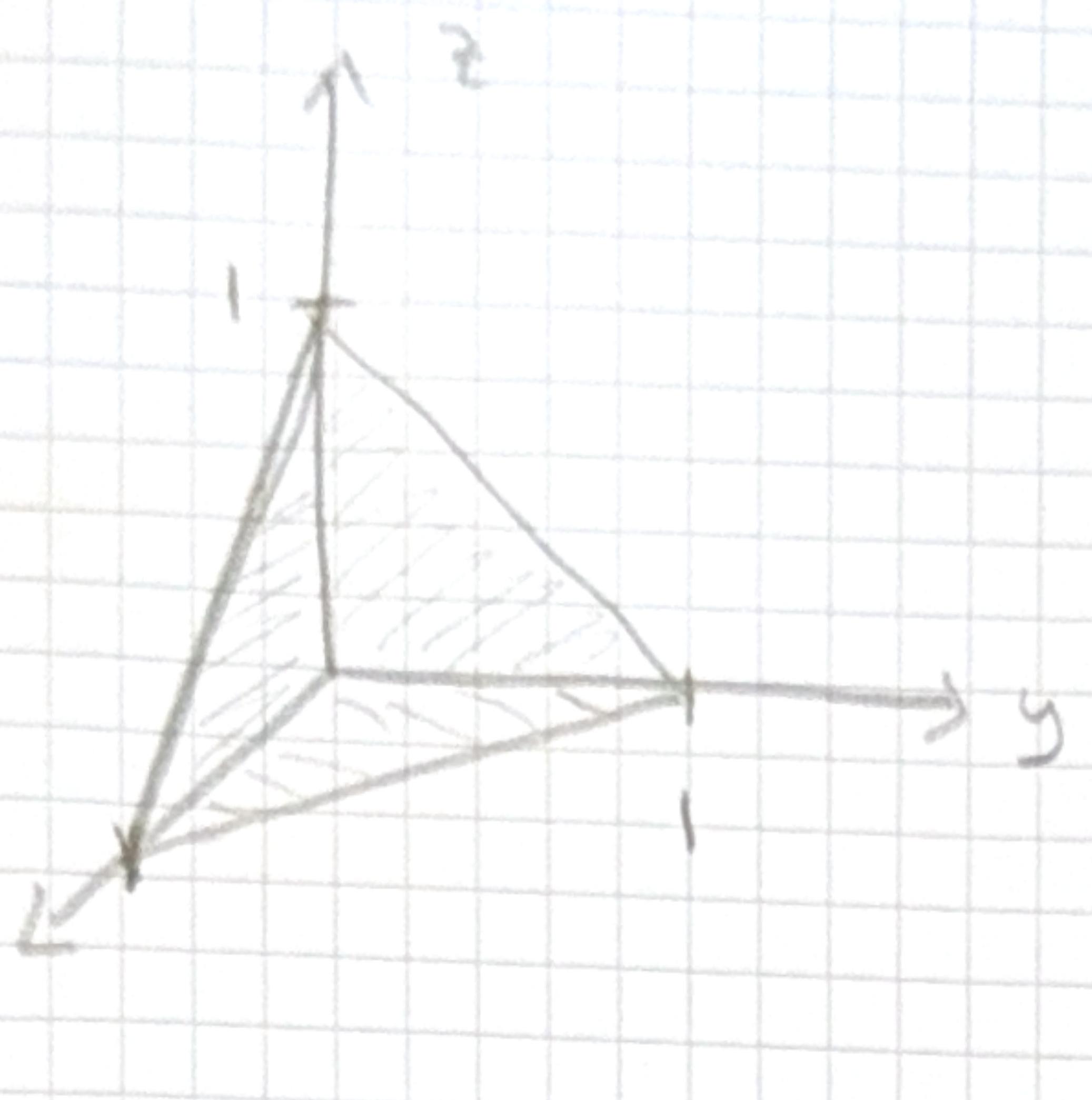
  1. Calculate the volume integral of the function \(T = z^2\) over the tetrahedron with corners at \((0,0,0), (1, 0, 0), (0,1,0), (0,0,1)\).

\[ \begin{aligned} \int_{V} T d \tau= & \int_{V} z^{2} d x d y d z \\ & =\iiint z^{2} d x d y d z \end{aligned} \]

If we integrate \(x\) first minimum is 0 max is at surface which is defined by \(x+y+z=1\). Thus, \(x=1-y-z\). Once \(x\) has been integrated \(y\) also has minimum of \(O\) and now max at line \(y+z=1\). Finally we have just \(z\) to consider which runs from 0 to 1 . \[ \begin{aligned} & \int_{0}^{1} \int_{0}^{1-z} \int_{0}^{1-z-y} z^{2} d x d y d z \\ & \left.\int_{0}^{1} \int_{0}^{1-z} z^{2} x\right|_{x=0} ^{x=1-z-y} d y d z \\ = & \int_{0}^{1} z^{2} \int_{0}^{1-z} 1-z-y d y d z \\ = & \left.\int_{0}^{1} z^{2}\left(y-z y-\frac{y^{2}}{2}\right)\right|_{0} ^{y=1-z} d z \\ = & \int_{0}^{1} z^{2}\left(1-z-z(1-z)-\frac{1}{2}(1-z)^{2}\right) d z \end{aligned} \] \[ \begin{aligned} & =\int_{0}^{1} z^{2}\left(1-z-2+z^{2}-\frac{1}{2}\left(1-2 z+z^{2}\right)\right) d z \\ & =\int_{0}^{1} z^{2}\left(1-2 z+z^{2}-\frac{1}{2}+z-\frac{z^{2}}{2}\right) d z \\ & =\int_{0}^{1} z^{2}\left(\frac{1}{2}-z+\frac{z^{2}}{2}\right) d z \\ & =\int_{0}^{1} \frac{z^{2}}{2}-z^{3}+\frac{z^{4}}{2} d z \\ & =\frac{z^{3}}{6}-\frac{z^{4}}{4}+\left.\frac{z^{5}}{10}\right|_{0} ^{1} \\ & =\frac{1}{6}-\frac{1}{4}+\frac{1}{10}=\frac{1}{60} \end{aligned} \]

15.2 Week 3

Question
  1. Check the fundamental theorem of gradients with the scalar function \(T = x^2 +4xy +2yz^3\). Assume point a is at the origin and point \(b = (1, 1, 1)\). Check the theorem for three paths:
  1. \((0,0,0) \rightarrow (1, 0, 0) \rightarrow (1, 1, 0) \rightarrow (1,1,1)\)
  2. \((0,0,0) \rightarrow (0, 0, 1) \rightarrow (0, 1, 1) \rightarrow (1,1,1)\)
  3. the parabolic path \(z=x^2\) and \(y=x\)

Part a) Path i) \((0,0,0) \rightarrow(1,0,0) \rightarrow(1,1,0) \rightarrow(1,1,1)\) \[ \begin{aligned} d \underline{l} & =d x \hat{x} \quad y=0, z=0 \\ \int_{\text {path i }} \nabla{T} \cdot d \underline{l} & =\int_{0}^{1} 2 x d x=\left.x^{2}\right|_{0} ^{1}=1 \end{aligned} \] \[ \begin{aligned} & \text { Path ii) } d\underline{l}=d y \hat{y} \quad x=1, z=0 \\ & \int_{\text {path } i i} \nabla T \cdot d \underline{l}=\int_{0}^{1} 4 d y=\left.4 y\right|_{0} ^{1}=4 . \end{aligned} \]

Path iii) \(d \underline{\ell}=d z \hat{z} \quad x=1, y=1\) \[ \int_{\text {path iii }} \nabla T \cdot d \underline{l}=\int_{0}^{1} 6 z^{2} d z=\left.2 z^{3}\right|_{0} ^{1}=2 \]

Total path \(1+4+2=7\)

Part b) \[ \begin{aligned} & (0,0,0) \rightarrow(0,0,1) \rightarrow(0,1,1) \rightarrow(1,1,1) \\ & \text { Path i} \quad d \underline{l}=d z \hat{z} \quad y=0, x=0 \\ & \int \nabla T \cdot d l=\int_{0}^{1} 0 d z=0 \end{aligned} \] \[ \begin{aligned} & \text { Path ii) } d \underline{l}=d y \hat{y} \quad x=0, z=1 \\ & \int \nabla T \cdot d \underline{l}=\int_{0}^{1} 2 d y=\left.2 y\right|_{0} ^{1}=2 \end{aligned} \] Path iii) \(\quad d \underline{l}=d x \hat{x} \quad y=1, z=1\) \[ \int \nabla T \cdot d \underline{l}=\int_{0}^{T} (2 x+4) d x=x^{2}+\left.4 x\right|_{0} ^{1}=5 \]

Total path 7.

Part c) parabolic path \(z=x^{2}, y=x \quad d x=d y \quad d z=2 x d x\) \[ \begin{aligned} & d \underline{l}=d x \hat{x}+d y \hat{y}+d z \hat{z} \\ \nabla T \cdot d \underline{l}= & (2 x+4 y) d x+\left(4 x+2 z^{3}\right) d y+6 y z^{2} d z \\ & =(2 x+4 x) d x+\left(4 x+2 x^{6}\right) d x+6 x x^{4} \cdot 2 x d x \\ & = (6 x + 4 x + 2 x^{6} + 12 x^{6}) d x. \\ & \int \nabla T \cdot d l=\int_{0}^{1}\left(10 x+ 14x^{6} \right)dx \\ & 5 x^{2}+\left.2 x^{7}\right|_{0} ^{1}=7 \end{aligned} \]

Question
  1. Compute the line integral of \(\mathbf{v} = 6\,\hat{x} + yz^2\,\hat{y} + (3y+z)\,\hat{z}\) along the triangular path \((0,0,0) \rightarrow (0, 1, 0) \rightarrow (0, 0, 2) \rightarrow (0,0,0)\). Check your answer using Stokes theorem.

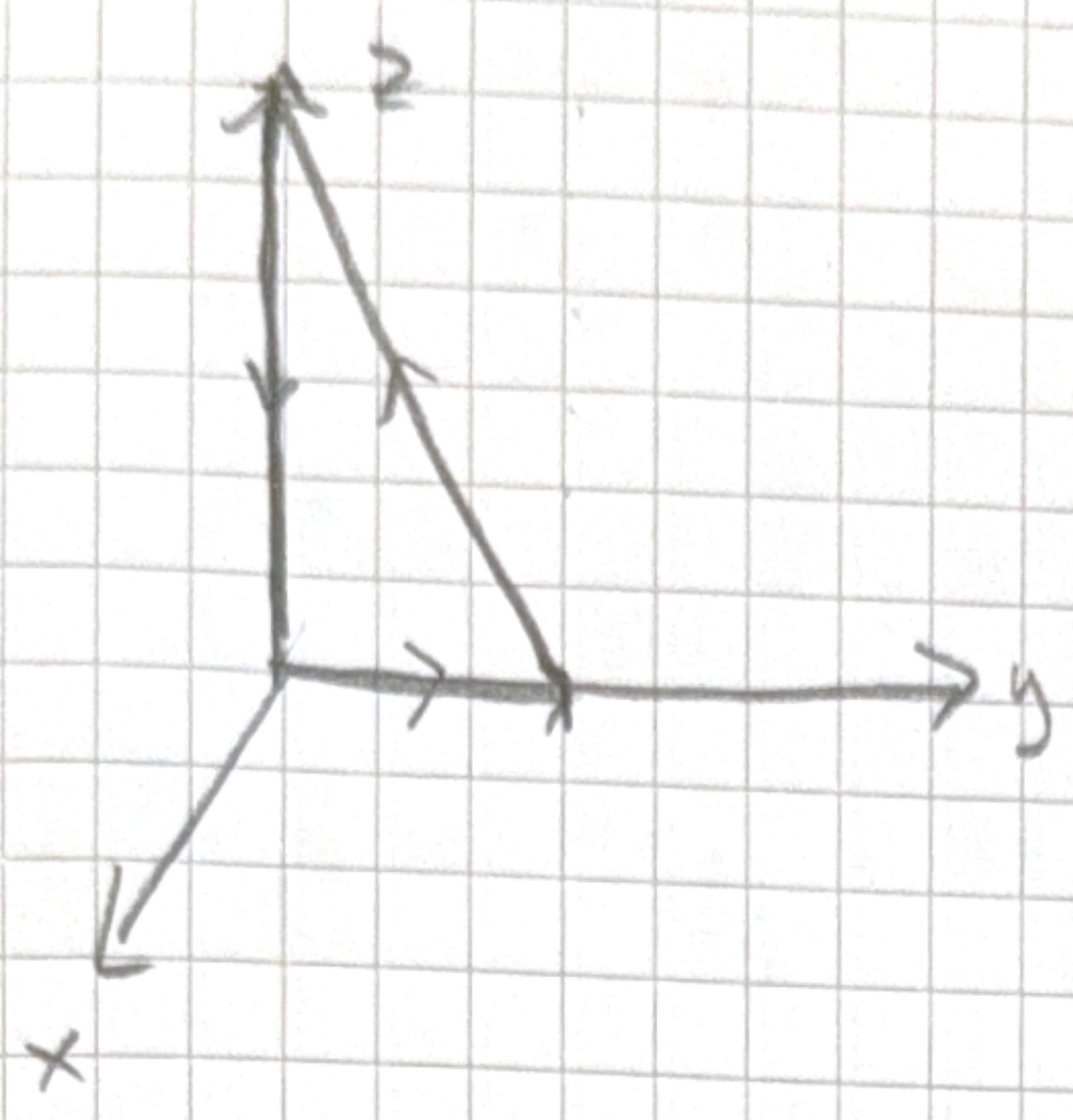
\[ \mathbf{v}=6 \hat{x}+y^{2} \hat{y}+(3 y+z) \hat{z} \]

\[ \begin{aligned} & (0,0,0) \rightarrow(0,1,0) \rightarrow(0,0,2) \\ & d \underline{l}=d x \hat{x}+d y \hat{y}+d z \hat{z} \end{aligned} \]

Path i \(x=0, z=0 \quad d \underline{l}=d y \hat{y}\) \[ \int \underline{v} \cdot d \underline{l}=\int y z^{2} d y\\ \int_{\text {path i }} \mathbf{v} \cdot d \underline{l}=\int_{0}^{1} 0=0 \]

\[ \begin{aligned} & \text { path ii } x=0 \quad d \underline{l}=d y \hat{y}+d z \hat{z} \\ &z=m y+b \\ &z=-2 y+2 \quad d z=-2 d y \\ & \int_{\text {path ii }} v \cdot d \underline{l}=\int y z^{2} d y+\int 3 y+z d z \\ & =\int y(-2 y+2)^{2} d y+\int(3 y+-2 y+2) \cdot-2 d y \\ & =\int_{1}^{0} 4 y^{3}-8y^2 + 4 y-2 y -4 d y \\ & =\int_{1}^{0} 4y^3-8y^2+2y-4 d y \\ & =-\frac{2}{3} \left.y^{4}-\frac{8}{3} y^3+y^2-4y\right|_{1} ^{0} \\ & =\frac{2}{3}+4=\frac{14}{3} \end{aligned} \]

\[ \begin{aligned} \text { part iii) } d \underline{l} & =d z \hat{z} \quad y=0, x=0 \\ \underline{v} \cdot d \underline{l} & =3 y+z d z \\ & =z d z \\ \int_{2}^{0} z d z & =\left.\frac{z^{2}}{2}\right|_{2} ^{0} \\ & =-2 \end{aligned} \]

Total path \[ \oint \mathbf{v} \cdot d\underline{l} = \frac{14}{3} - \frac{6}{3} = \frac{8}{3} \]

Check with Stokes Theorem:

\[ \begin{aligned} & \int_{s}(\nabla \times \underline{v}) \cdot d \underline{a} \\ & \left|\begin{array}{ccc} \hat{x} & \hat{y} & \hat{z} \\ \partial / \partial x & \partial / \partial y & \partial / \partial z \\ 6 & y z^{2} & 3 y+z \end{array}\right| \\ & =\hat{x}(3-2 y z)-\hat{y}(0-0)+\hat{z}(0-0) \\ & =\left(3-2 y^{2}\right) \hat{x} \\ & \iint (3-2 y z) d y d z \quad z=-2 y+2 \\ & \int_{0}^{1}\left[\int_{0}^{-2 y+2} 3-2 y z d z\right] d y \\ & \int_{0}^{1}\left[3 z-\left.y z^{2}\right|_{z=0} ^{z=2-2 y}\right] d y \\ & \int_{0}^{1} 6-6 y-y(2-2 y)^{2} d y \\ & 6 y-5 y^{2}+\frac{8}{3} y^{3}-\left.y^{4}\right|_{0} ^{1} \\ & 6-6 y-y\left(4-8 y+4 y^{2}\right) d y \\ & \int_{0}^{1} 6-6 y-4 y+8 y^{2}-4 y^{3} d y \\ & 6-5+\frac{8}{3}-1 \\ & =\frac{8}{3} \end{aligned} \]

Question
  1. If \(\mathbf{A}\) and \(\mathbf{B}\) are vector functions what does (\(\mathbf{A}\cdot \nabla) \mathbf{B}\) mean? (What are the x, y, and z components?)
  2. Compute (\(\hat{r}\cdot \nabla) \hat{r}\).
  3. For the functions from problem 3 in week 2 evaluate (\(\mathbf{v_a}\cdot \nabla) \mathbf{v_b}\)
Question
  1. Test the divergence theorem for the function \(\mathbf{v} = xy\, \hat{x}+ 2yz\,\hat{y}+3zx\,\hat{z}\). Take for the volume a cube placed ath the origin with sides of length 2.

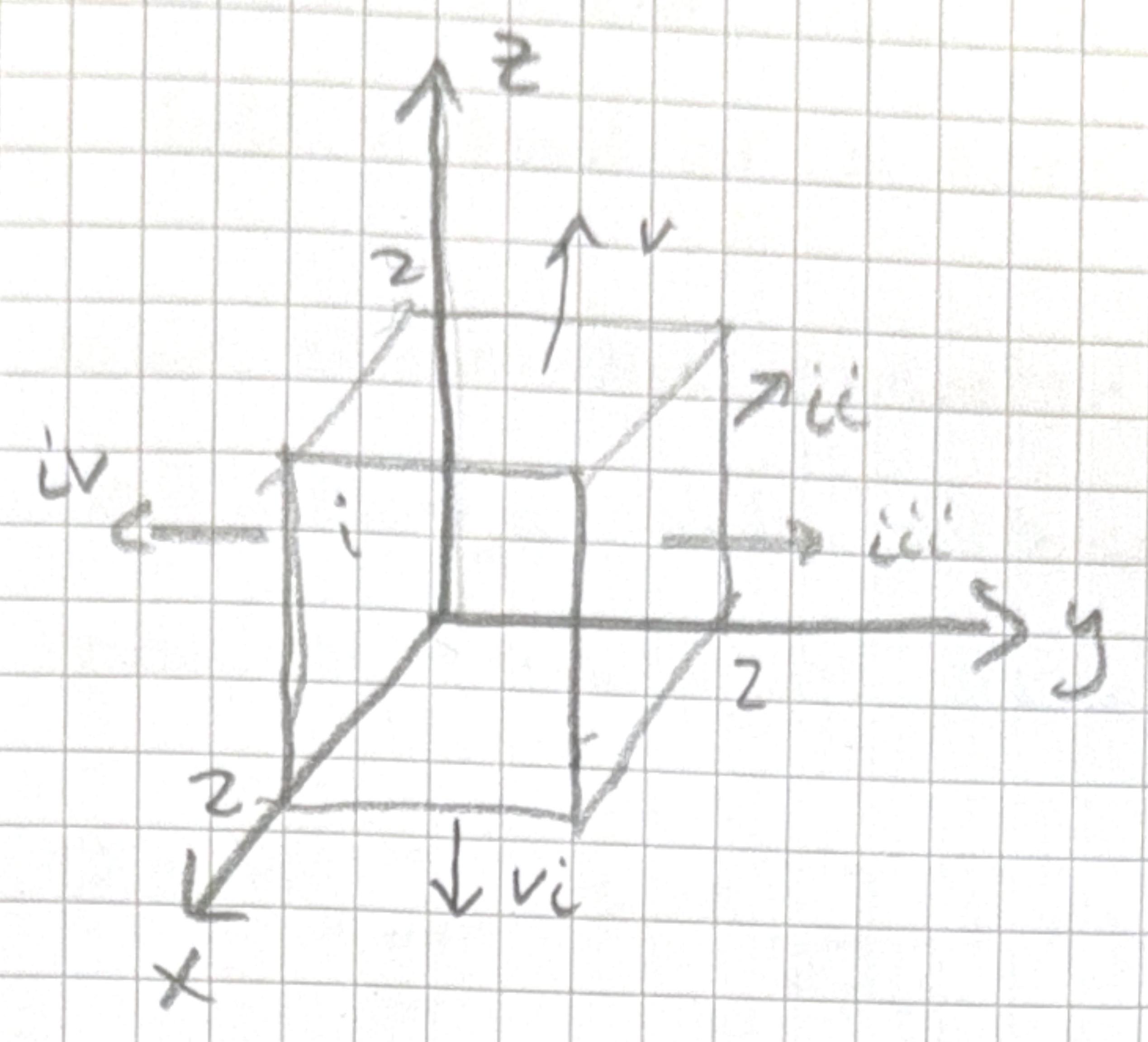
\(\quad \underline{v}=x y \hat{x}+2 y z \hat{y}+3 z x \hat{z}\) \[ \begin{gathered} \int_{V}(\nabla \cdot \underline{v}) d \tau=\oint_{s} \underline{v} \cdot d \underline{a} \\ \nabla \cdot \underline{v}=y+2 z+3 x \\ d \tau=d x d y d z \\ \int_{0}^{2} \int_{0}^{2} \int_{0}^{2}(y+2 z+3 x) d x d y d z \\ \int_{0}^{2} \int_{0}^{2} y x+2 z x+\left.\frac{3 x^{2}}{2}\right|_{x=0} ^{x=2} d y d z \\ \iint_{0}^{2}(2 y+4 z+6) d y d z \\ \int_{0}^{2} y^{2}+4 z y+\left.6 y\right|_{y=0} ^{y=z} d z \\ \int_{0}^{2} 4+8 z+12 d z \\ 16 z+\left.4 z^{2}\right|_{0} ^{2} \\ 3 z+16=48 \end{gathered} \] i) \(d \underline{a}=d y d z \hat{x}\) \[ \begin{aligned} & \quad \underline{v} \cdot \underline{a}=x y d y d z \\ & \int_{0}^{2} \int_{0}^{2} x y d y d z \\ & =\left.\int_{0}^{2} \frac{x y^{2}}{2}\right|_{y=0} ^{y=2} d z \\ & \int_{0}^{2} 2 x d z \\ & =\left.2 x z\right|_{0} ^{2} \quad x=2 \\ & =8 . \end{aligned} \] (ii) \(d \underline{a}=-d y d z \hat{x} \quad x=0\) \[ \int_{0}^{2} \int_{0}^{2} x y d y d z=0 . \] iii) \(d \underline{a}=d x d z \hat{y} \quad y=2\). \[ \begin{aligned} & \underline{v} \cdot d \underline{a}=2 \cdot 2 z d x d z \\ & \int_{0}^{2} \int_{0}^{2} 4 z d x d z \\ & \left.\int_{0}^{2} 4 z x\right|_{x=0} ^{x=2} d z \\ & \int_{0}^{2} 8 z d z \\ & \left.4 z^{2}\right|_{0} ^{2}=16 \end{aligned} \] (iv) \(d \underline{a}=-d x d z \hat{y} \quad y=0\) \[ \int_{0}^{2} \int_{0}^{2} 0 d x d z=0 \] v) \(d \underline{a}=d x d y \hat{z} \quad z=2\) \[ \begin{aligned} & \int_{0}^{2} \int_{0}^{2} 6 x d x d y \\ & \left.\int_{0}^{2} 3 x^{2}\right|_{x=0} ^{x=2} d y \\ & =\left.12 y\right|_{0} ^{2}=24 . \end{aligned} \] \[ \begin{aligned} & \text { vi) } d \underline{a}=-d x d y \hat{z} z=0 \\ & \int_{\delta} 0 d x d y=0 \\ & \therefore \oint_{S} \underline{v} \cdot d \underline{a}=48 \cdot \end{aligned} \]

Question
  1. Test Stokes theorem for the \(\mathbf{v}\) in problem 4. Take the path to be three segments that make a triangular loop: \((0,0,0) \rightarrow (0, 2, 0) \rightarrow (0, 0, 2) \rightarrow (0,0,0)\).

\[ \begin{aligned} & \int_{S}(\nabla \times \underline{v}) \cdot d \underline{a}=\oint_{P} \underline{v} \cdot d \underline{l} \\ \end{aligned} \] Right hand side first: \[ \begin{aligned} & v=x y \hat{x}+2 y z \hat{y}+3 z x \hat{z} \\ & \nabla \times \underline{v}=\left|\begin{array}{ccc} \hat{x} & \hat{y} & \hat{z} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ x y & 2 y z & 3 x z \end{array}\right| \\ & =\hat{x}(0-2 y)-\hat{y}(3 z-0)+\hat{z}(0-x) \\ & =-2 y \hat{x}-3 z \hat{y}-x \hat{z} \\ & m y+b=z \\ & d \underline{a}=d y d z \hat{x} \\ & z=-y+2 \\ & \iint(-2 y \hat{x}-3 z \hat{y}-x \hat{z}) \cdot d y d z \hat{x} \\ & =\int_{y=0}^{y=2} \int_{z=0}^{z=2-y}-2 y d z d y \\ & \int_{0}^{2}-\left.2 y z\right|_{z=0} ^{z=2-y} d y \\ & \int_{0}^{2}-2 y(2-y) d y \\ & -\int_{0}^{2} 4 y-2 y^{2} d y \\ & -\left(2 y^{2}-\left.\frac{2 y^{3}}{3}\right|_{0} ^{2}\right) \\ & -\left(8-\frac{16}{3}\right) \\ & -\frac{24-16}{3}=-\frac{8}{3} \end{aligned} \]

Now for the path side …

Section 1 of the path: \[ \begin{aligned} & d \underline{l}=d y \hat{y} \quad x=0, z=0 \\ & \underline{v} \cdot d \underline{l} =2 y z=0 \\ & \int_{0}^{2} 2 y z d y=\int_{0}^{2} 0=0 \end{aligned} \]

Part 2 of path: \[ \begin{aligned} &x=0, \quad d \underline{l}=d y \hat{y}+d z \hat{z} \quad z=-y+2 \quad d z=- d y\\ & \int 2 y z d y+\int^{3 x z d z} \\ & \int_{2}^{0} 2 y(-y+2) d y \\ & \int_{2}^{0}-2 y^{2}+4 y d y \\ & -\frac{2}{3} y^{3}+\left.2 y^{2}\right|_{2} ^{0} \\ & \frac{2}{3} \cdot 8-8 \\ & \frac{16}{3}-\frac{24}{3}=-\frac{8}{3} \end{aligned} \] Part 3 of path: \[ \begin{aligned} & d \underline{l}=d z \hat{z} \quad x=0, y=0 \\ & \int \underline{v} \cdot d \underline{l}=\int_{2}^{0} 3 z x d z=0 \end{aligned} \] So total path \[ \oint_{p} \underline{v} \cdot d \underline{l}=-\frac{8}{3} . \]

Question
  1. Prove that the divergence of the curl is always zero. Check it for the function \(\mathbf{v_a}\) of problem 3 in week 2.

\[ \begin{aligned} & \nabla \cdot(\nabla \times \mathbf{v}) \\ & \nabla \times \mathbf{v}=\left|\begin{array}{ccc} \hat{x} & \hat{y} & \hat{z} \\ \partial/ \partial x & \partial /\partial y & \partial /\partial z \\ v_{x} & v_{y} & v_{z} \end{array}\right| \\ & =\hat{x}\left(\partial v_{z} / \partial y-\partial v_{y} / \partial z\right) \\ & -\hat{y}\left(\partial v_{z} / \partial x-\partial v_{x} / \partial z\right) \\ & +\hat{z}\left(\partial v_{y} / \partial x-\partial v_{x} / \partial y\right) \\ & =\hat{x}\left(\frac{\partial v_{z}}{\partial y}-\frac{\partial v_{y}}{\partial z}\right)+\hat{y}\left(\frac{\partial v_{x}}{\partial z}-\frac{\partial v_{z}}{\partial x}\right)+\hat{z}\left(\frac{\partial v_{y}}{\partial x}-\frac{\partial v_{y}}{\partial y}\right) \\ & \nabla \cdot(\nabla \times \mathbf{v}) \\ & =\frac{\partial}{\partial x}\left(\frac{\partial v_{z}}{\partial y}-\frac{\partial v_{y}}{\partial z}\right)+\frac{\partial}{\partial y}\left(\frac{\partial v_{x}}{\partial z}-\frac{\partial v_{z}}{\partial x}\right)+\frac{\partial}{\partial z}\left(\frac{\partial v_{y}}{\partial z}-\frac{\partial v_x}{\partial y}\right) \\ & \frac{\partial^{2} v_{z}}{\partial x \partial y}-\frac{\partial^{2} v_{y}}{\partial x \partial z}+\frac{\partial^{2} v_{x}}{\partial y \partial z}-\frac{\partial^{2} v_{z}}{\partial x \partial y}+\frac{\partial^{2} v_{y}}{\partial x \partial z}-\frac{\partial^{2} v_{x}}{\partial z \partial y} \\ & =0 \text {. } \end{aligned} \]

Question
  1. Prove that the curl of the gradient is always zero.

\[ \begin{aligned} & \nabla \times \nabla T \\ & \nabla T=\frac{\partial T}{\partial x} \hat{x}+\frac{\partial T}{\partial y} \hat{y}+\frac{\partial T}{\partial z} \hat{z} \\ & \nabla \times \nabla T=\left|\begin{array}{ccc} \hat{x} & \hat{y} & \hat{z} \\ \partial / \partial x & \partial / \partial y & \partial /\partial z \\ \frac{\partial T}{\partial x} & \frac{\partial T}{\partial y} & \frac{\partial T}{\partial z} \end{array}\right| \\ &=\hat{x}\left(\frac{\partial^{2} T}{\partial y \partial z}-\frac{\partial^{2} T}{\partial y \partial z}\right)-\hat{y}\left(\frac{\partial^{2} T}{\partial x \partial z}-\frac{\partial^{2} T}{\partial x \partial z}\right) \\ &+\hat{z}\left(\frac{\partial^{2} T}{\partial x \partial y}-\frac{\partial^{2} T}{\partial x \partial y}\right)=0 \end{aligned} \]

Question
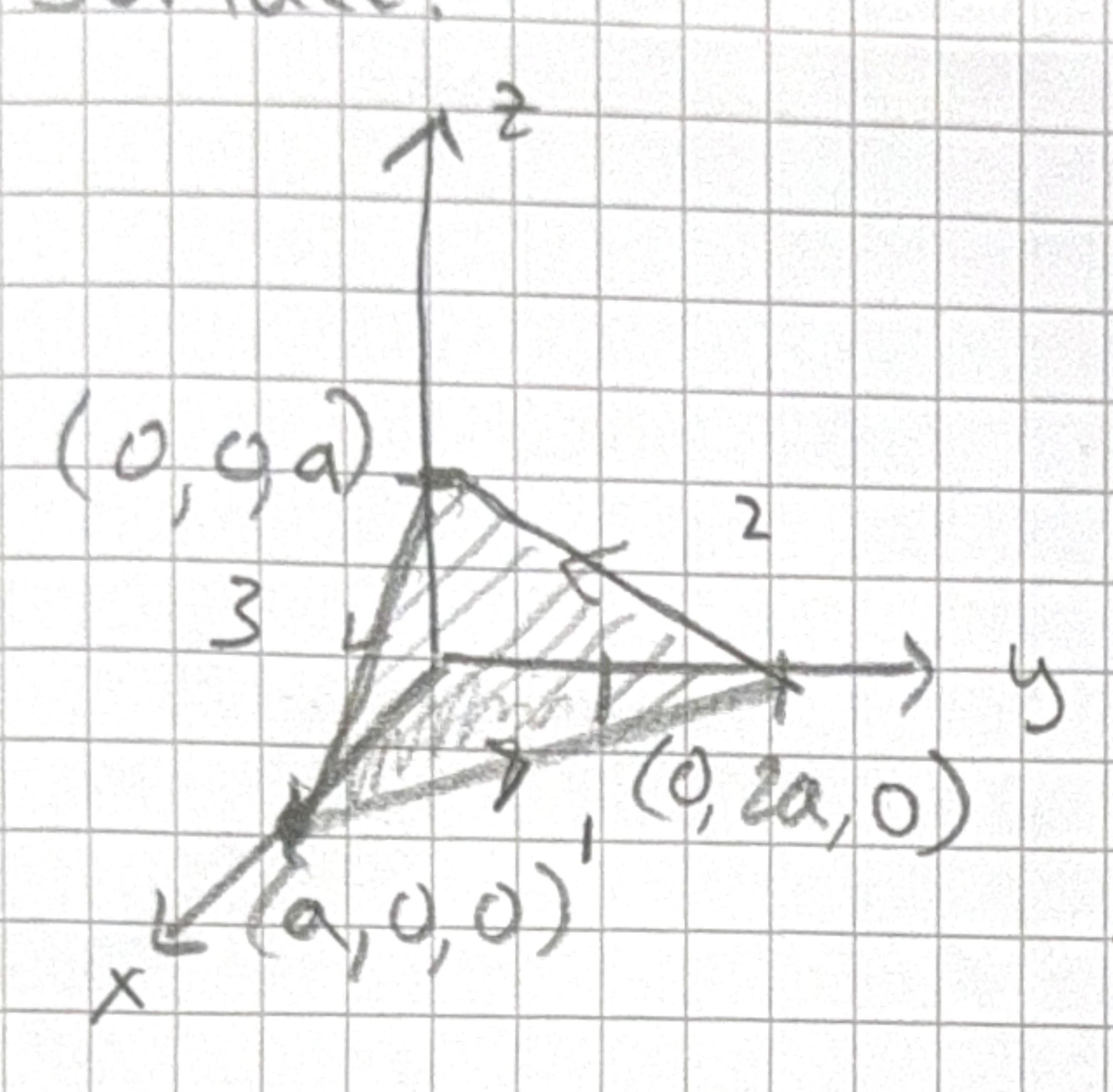
  1. Use Stokes theorem to find the surface integral \(\mathbf{v} = y\,\hat{z}\) for the triangular surface defined by the vertices \((a, 0, 0), (0,2a,0), (0,0,a)\). Hint one side of Stokes theorem will be much more straight forward than the other.

\[ \begin{aligned} & \underline{v}=y \hat{z} \\ & \int_{S}(\nabla \times \underline{v}) \cdot d \underline{a}=\oint_{p} \underline{v} \cdot d \underline{l} \end{aligned} \]

Surface:

\[ \begin{aligned} & \left|\begin{array}{ccc} \hat{x} & \hat{y} & \hat{z} \\ \frac{\partial}{\partial x} & {\partial}{\partial y} & {\partial}{\partial z} \\ 0 & 0 & y \end{array}\right| \\ & \quad=\hat{x}(1)-\hat{y} 0+\hat{z} 0 \\ & \nabla \times \underline{v}=\hat{x} \end{aligned} \]

\[ \begin{array}{ll} \text { Part 1: } d \underline{l}=d x \hat{x}+d y \hat{y} \quad z=0 \quad d z=0 \\ \int y \hat{z} \cdot(d x \hat{x}+d y \hat{y})=0 \end{array} \]

Part 2: \(d \underline{l}=d y \hat{y}+d z \hat{z} \quad x=0\)

\[ \begin{aligned} & z=m y+b \\ & z=-1 / 2 y+b \\ & z=-1 / 2 y+1 \\ & d z=-1 / 2 d y \end{aligned} \] \[ \begin{aligned} & \int y \hat{z} \cdot(d y \hat{y}+d z \hat{z}) \\ & \int y d z=\int_{2 a}^{0} y \cdot-1 / 2 d y \\ = & -\left.\frac{1}{2} \frac{y^{2}}{2}\right|_{2 a} ^{0} \\ = & \frac{1}{4} 4 a^{2}=a^{2} \end{aligned} \]

Part 3: \(d \underline{l}=d x \hat{x}+d \hat{z} \quad y=0\), \[ \int y \hat{z} \cdot(d x \hat{x}+d z \hat{z})=0 \]

15.3 Week 4

Question
  1. \(r = e^{-p^2-q^2}\), \(p = e^s\), \(q = e^{-s}\). Find \(\frac{dr}{ds}\).

There are several ways to do this - here is one way: \[ \begin{aligned} \frac{dr}{ds} &= \frac{\partial r}{\partial p} \frac{dp}{ds} + \frac{\partial r}{\partial q} \frac{dq}{ds}\\ \frac{\partial r}{\partial p} &= e^{-p^2-q^2} \cdot -2p\\ \frac{\partial r}{\partial q} &= e^{-p^2-q^2} \cdot -2q\\ \frac{dp}{ds} &= e^s\\ \frac{dq}{ds} &= -e^{-s} \end{aligned} \] Substitute all of this into the full derivative \[ \begin{aligned} \frac{dr}{ds} &= -2pe^{-p^2-q^2}\cdot e^s + (-2q)e^{-p^2-q^2}\cdot -e^{-s}\\ &= (-2pe^s+2qe^{-s})e^{-p^2-q^2}\\ &=2r(q^2-p^2) \end{aligned} \]

Question
  1. \(c = \sin (a - b)\), \(b = ae^{2a}\). Find \(\frac{dc}{da}\).

\[ \begin{aligned} \frac{dc}{da} &= \frac{\partial c}{\partial b} \cdot \frac{db}{da} + \frac {\partial c}{\partial b} \cdot \frac{da}{da}\\ \frac{\partial c}{\partial b} &= \cos(a-b)\cdot-1\\ \frac{\partial c}{\partial a} &= \cos(a-b)\\ \frac{db}{da} &= e^{2a}+ae^{2a}\cdot 2 = e^{2a}(1+2a)\\ \therefore \frac{dc}{da} &= \cos (a-b)(1-2b-e^{2a}) \end{aligned} \]

Question
  1. \(z = x^2 +2y^2\)
    1. Find \(\left(\frac{\partial z}{\partial x}\right)_y\).
    2. Write \(x\) and \(y\) in plane polar coordinates (in terms of \(r\) and \(\theta\)) and find \(\left(\frac{\partial z}{\partial x}\right)_r\).
  1. Take the partial derivative of \(z\) keeping \(y\) constant: \(\left(\frac{\partial z}{\partial x}\right)_y = 2x\).
  2. There are several approaches to this problem - here is mine. First write \(x\) and \(y\) in plane polar coordinates: \[ \begin{aligned} x &= r\cos\theta \quad y = r\sin\theta \end{aligned} \] Since we want the partial of \(z\) with respect to \(x\) while keeping \(r\) constant lets take the opportunity to substitute for \(y\) in terms of \(\theta\) and \(r\). \[ \begin{aligned} z&=x^2+2y^2\\ z&=x^2 + 2r^2\sin^2\theta \end{aligned} \] We can substitute again to get rid of the \(\theta\) \[ \begin{aligned} \sin^2 \theta &= 1-\cos^2 \theta\\ \cos \theta &= \frac{x}{r} \quad \cos^2 \theta = \frac{x^2}{r^2}\\ \sin^2 \theta &= 1 - \frac{x^2}{r^2}\\ z&= x^2 + 2r^2\left(1 - \frac{x^2}{r^2}\right)\\ &= -x^2 - 2r^2\\ \therefore \left(\frac{\partial z}{\partial x}\right)_r &= -2x \end{aligned} \]
Question
  1. Solve \[ \int^1_{x=0} \int^4_{y=2} 3x\, dx dy \]

\[ \begin{aligned} \int^1_{x=0} 3x\, dx \int^4_{y=2}dy\\ \left.\left.\frac{3}{2}x^2\right|^1_0\cdot y\right|^4_2 = 3 \end{aligned} \]

Question
  1. Solve \[ \int^2_{y=0} \int^4_{x=2y} dx dy \]

\[ \begin{aligned} \int^2_{y=0} (4-2y) dy\\ \left. 4y-y^2\right|_0^2 = 4 \end{aligned} \]

Question
  1. Solve \[ \int^1_{x=0} \int^{e^x}_{y=x} y\, dx dy \]

\[ \begin{aligned} =&\left.\int_{x=0}^1 \frac{y^2}{2}\right|_x^{e^x} \,dx\\ =&\frac{1}{2}\int_0^1(e^{2x}-x^2)dx\\ =&\left.\frac{1}{2}(\frac{e^{2x}}{2}-\frac{x^3}{3})\right|_0^1 = \frac{e^2}{4} - \frac{5}{12} \end{aligned} \]

Question
  1. \(\iint\limits_A (2x - 3y)\, dx dy\), where \(A\) is the triangle with vertices \((0,0), (2, 1), (2, 0)\).

The hypotenuse of the triangle is the line \(y=\frac{1}{2}x\). Lets integrate over \(y\) first keeping \(x\) constant. \[ \begin{aligned} \int_{x=0}^2\int_{y=0}^{\frac{x}{2}}(2x-3y)\,dydx\\ \left.\int_{x=0}^2(2xy-\frac{3}{2}y^2)\right|_{y=0}^{\frac{x}{2}}dx\\ \int_0^2\frac{5}{8}x^2\,dx = \frac{5}{3} \end{aligned} \]

Question
  1. Solve \[ \iint 2xy\, dx dy \]

over the triangle \((0,0), (2,1), (3,0)\).

I split this into two right triangles. One with \(x\) ranging from 0 to 2 with area \(A_1\) and a hypotenuse \(y=x/2\) and one with \(x\) ranging from 2 to 3, area \(A_2\) and a hypotenuse \(y=3-x\). \[ \begin{aligned} &= \iint_{A_1} 2xy\,dxdy + \iint_{A_2} 2xy\,dxdy\\ &=\int_{x=0}^2\int_{y=0}^\frac{x}{2} 2xy\,dydx + \int_{x=2}^3\int_{y=0}^{3-x} 2xy\,dydx\\ &=\left.\int_0^2 x y^2\right|_{y=0}^{\frac{x}{2}} dx + \left.\int_2^3 x y^2\right|_{y=0}^{3-x} dx\\ &= \int_0^2 x\cdot \frac{x^2}{4}dx + \int_0^3 x(3-x)^2 dx\\ &= \int_0^2 \frac{x^3}{4}dx +\int_2^3 x(9-6x+x^2)dx\\ &= \left.\frac{x^4}{16}\right|_0^2 + \int_2^3(9x-6x^2+x^3)dx\\ &= 1 + \left.\left(\frac{9x^2}{3}-\frac{6x^3}{3}+\frac{x^4}{4}\right)\right|_2^3 = \frac{7}{4} \end{aligned} \]

Question
  1. Solve \[ \int_{x=1}^2\int_{y=x}^{2x}\int_{z=0}^{y-x} dz dy dx \]

\[ \begin{aligned} &=\int_{x=1}^2\int_{y=x}^{2x}(y-x)\,dydx\\ &=\left.\int_1^2\left(\frac{y^2}{2}-xy\right)\right|_x^{2x}\\ &=\int_1^2\frac{x^2}{2}\,dx = \frac{7}{6} \end{aligned} \]

15.4 Week 5 (due 12:30pm Friday 18 Oct)

  1. Calculate the Laplacian of \(\ln (x^2 +y^2)\).

  2. Is \(\mathbf{F} = y\hat{i} + xz\hat{j} +z\hat{k}\) a conservative field? Justify your answer.

    Evaluate \(\int \mathbf{F}\cdot d\mathbf{r}\) from \((0,0,0)\) to \((1,1,1)\) along two paths:

    1. a broken line \((0,0,0)\rightarrow (1,0,0) \rightarrow (1,1,0) \rightarrow (1,1,1)\)
    2. a straight line

  3. Given \(\phi = z^3 -3xy\)

    1. find grad \(\phi\)
    2. find the directional derivative of \(\phi\) at the point(1, 2,3) in the direction \(\hat{i}+\hat{j}+\hat{k}\)

  4. Let \(\mathbf{v} = x\hat{i}+y\hat{j}+z\hat{k}\). Evaluate \(\oint_S \mathbf{v}\cdot d\mathbf{a}\) over the closed surface of a cylinder of hight \(h\) and radius \(a\) with a base centred at the origin. (Hint: consider using the divergence theorem.)

  5. Calculate the volume of the region bounded by the planes \(z = 2x+3y+6\) and \(z= 2x+7y+8\) and the triangle with vertices \((0,0), (0,3),\) and \((2,1)\) projected in the vertical direction (taken as the z-direction).