12  General derivation of \(\nabla\) operator

Define a point in space \(u, v, w\) in Cartesian it would be \((x, y, z)\) in cylindrical it is \((s, \phi, z)\) and in spherical \((r, \theta, \phi)\). The general coordinate system must be mutually orthogonal call it \(\hat{u}, \hat{v}, \hat{w}\). An infinitesimal displacement: \(d\mathbf{l}= f du\hat{u}+ g d v \hat{v}+h d w \hat{w}\). \(f\), \(g\), \(h\) are functions of position characteristic of the particular coordinate system in Cartesian \(f=g=h=1\). In cylindrical \(f=h=1\) and \(g=s\).

12.1 Gradient

If you move from point \(u, v, w\) to \(u+d u, v+d v, w+d w\) a scalar function \(t(u, v, w)\) varies by (partial differential) \[ \begin{aligned} d t &=\frac{\partial t}{\partial u} d u+\frac{\partial t}{\partial v} d v+\frac{\partial t}{\partial w} d w \end{aligned} \] We can write this as a dot product: \[ \begin{aligned} & d t=\nabla t \cdot d \mathbf{l}=\nabla t_{u} f d u+\nabla t_{v} g d v+\nabla t_{w} h d w \\ & \text { if } \nabla t_{u}=\frac{1}{f} \frac{\partial t}{\partial u}, \nabla t_{v}=\frac{1}{g} \frac{\partial t}{\partial v}, \nabla t_{w}=\frac{1}{h} \frac{\partial t}{\partial w} \end{aligned} \]

This would mean the gradient would be \[ \nabla t=\frac{1}{f} \frac{\partial t}{\partial u} \hat{u}+\frac{1}{g} \frac{\partial t}{\partial v} \hat{v}+\frac{1}{h} \frac{\partial t}{\partial w} \hat{w} \] Now what would that mean for our coordinate systems? For cartesian \(f=g=h=1\) so \[ \nabla t=\frac{\partial t}{\partial x} \hat{x}+\frac{\partial t}{\partial y} \hat{y}+\frac{\partial t}{\partial z} \hat{z} \] for cylindrical \(f=h=1\) and \(g=s\) \[ \nabla t=\frac{\partial t}{\partial s} \hat{s}+\frac{1}{s} \frac{\partial t}{\partial \phi} \hat{\phi}+\frac{\partial t}{\partial z} \hat{z} \]

Lets just check that this general definition satisfies the theorem ot gradients. The total change in \(t\) as you go from point \(a\) to \(b\) \[ \begin{aligned} \int_{a}^{b} d t & =\int_{a}^{b}(\nabla t) \cdot d \mathbf{l} \\ & =t(b)-t(a) \end{aligned} \] and is by definition path independent.

12.2 Divergence

Lets define a vector: \[ \mathbf{A}(u, v, w)=A_{u} \hat{u}+A_{v} \hat{v}+A_{w} \hat{w} \]

We need to evaluate \(\oint \mathbf{A}\cdot d\mathbf{a}\) over a surface of infinitesimal volume generated at a point \(u, v, w\)

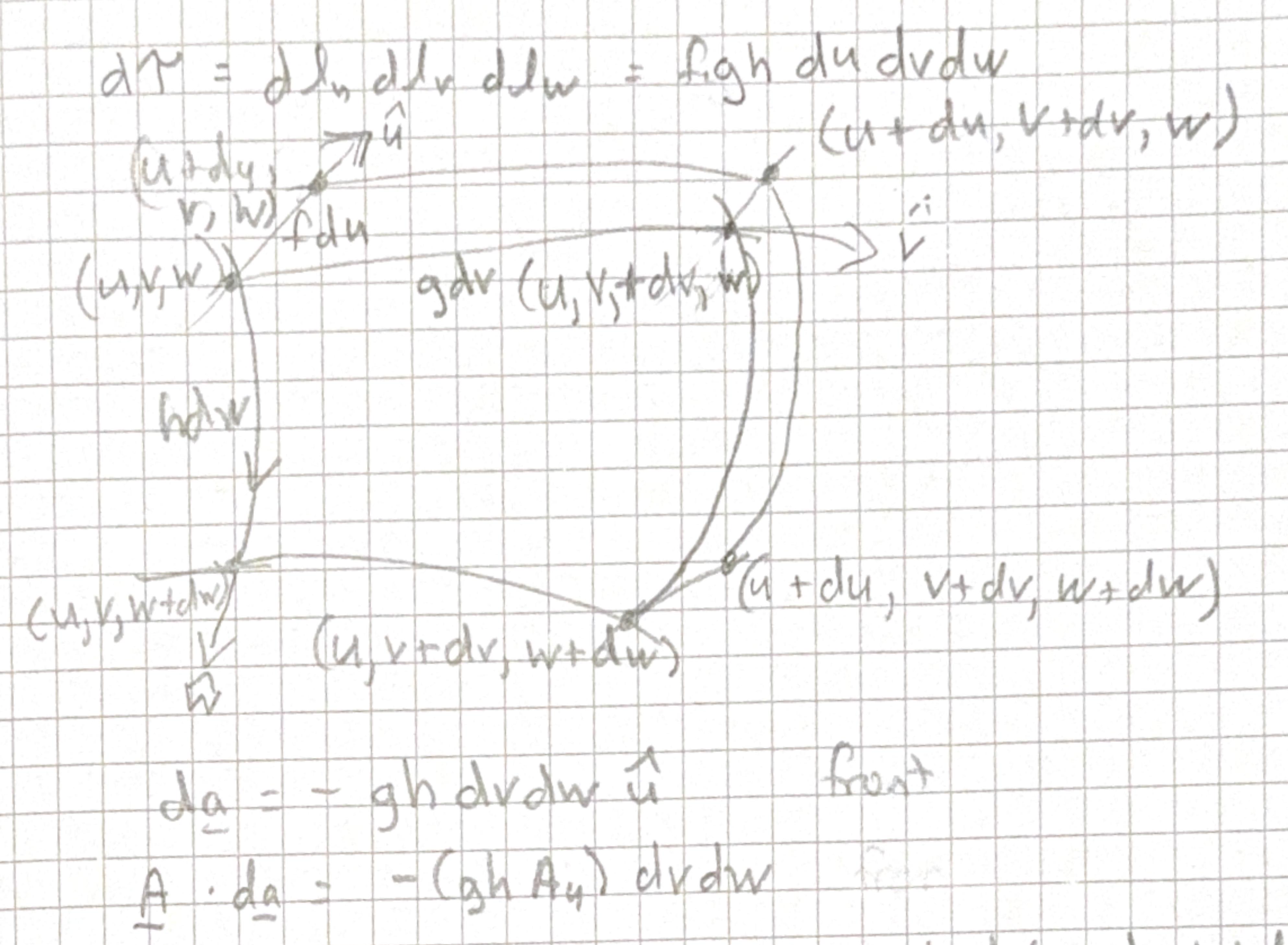
back has opposite sign and is evaluated at \(u+du\)

\[ \begin{aligned} F(u+d u)-F(u)&=\frac{d F}{d u} d u\\ \frac{\partial}{\partial u}\left(g h A_{u}\right) d u d v d w&=\frac{1}{f g h} \frac{\partial}{\partial u}\left(g h A_{u}\right) d \tau \end{aligned} \] left and right hand sides yield \[ \frac{\partial}{\partial v}\left(f h A_{v}\right) d u d v d w=\frac{1}{f g h} \frac{\partial}{\partial v}\left(f h A_{v}\right) d \tau \] and top and bottom \[ \frac{\partial}{\partial w}\left(f_{g} A_{w}\right) d u d v d w=\frac{1}{f_{g h}} \frac{\partial}{\partial w}\left(f_{g} A_{w}\right) d T \]

Then all together \[ \begin{aligned} & \oint \mathbf{A} \cdot d \mathbf{a}=\frac{1}{f g h}\left[\frac{\partial}{\partial u}\left(g h A_{u}\right)+\frac{\partial}{\partial v}\left(f h A_{v}\right)+\frac{\partial}{\partial w}\left(fg A_{w}\right)\right] d\tau\\ & \left.\nabla \cdot \mathbf{A}=\frac{1}{f g h}\left[\frac{\partial}{\partial u}\left(g h A_{u}\right)+\frac{\partial}{\partial v}\left(f h A_{v}\right)+\frac{\partial}{\partial w}\left(fg A_{w}\right)\right]\right] \end{aligned} \]

Over finite \(\oint \mathbf{A} \cdot d \mathbf{a}=\int(\nabla \cdot \mathbf{A}) d \tau\)

For cylindrical coordinates the divergence is: \[ \begin{aligned} & \nabla \cdot \mathbf{A}=\frac{1}{s}\left(\frac{\partial}{\partial s} s A_{s}+\frac{\partial}{\partial \phi} A_{\phi}+\frac{\partial}{\partial z} s A_{z}\right) \\ & \nabla \cdot \mathbf{A}=\frac{1}{s} \frac{\partial\left(s A_{s}\right)}{\partial s}+\frac{1}{s} \frac{\partial}{\partial \phi} A_{\phi}+\frac{\partial}{\partial z} A_{z} \end{aligned} \]

12.3 Curl

Remember the fundamental theorem of curls: \[ \int_S (\nabla \times \mathbf{v}) \cdot d\mathbf{a} = \oint_P \mathbf{v} \cdot d\mathbf{l}. \] So if we start with the right hand side the line integral \(\oint \mathbf{A} \cdot d \mathbf{\ell}\)

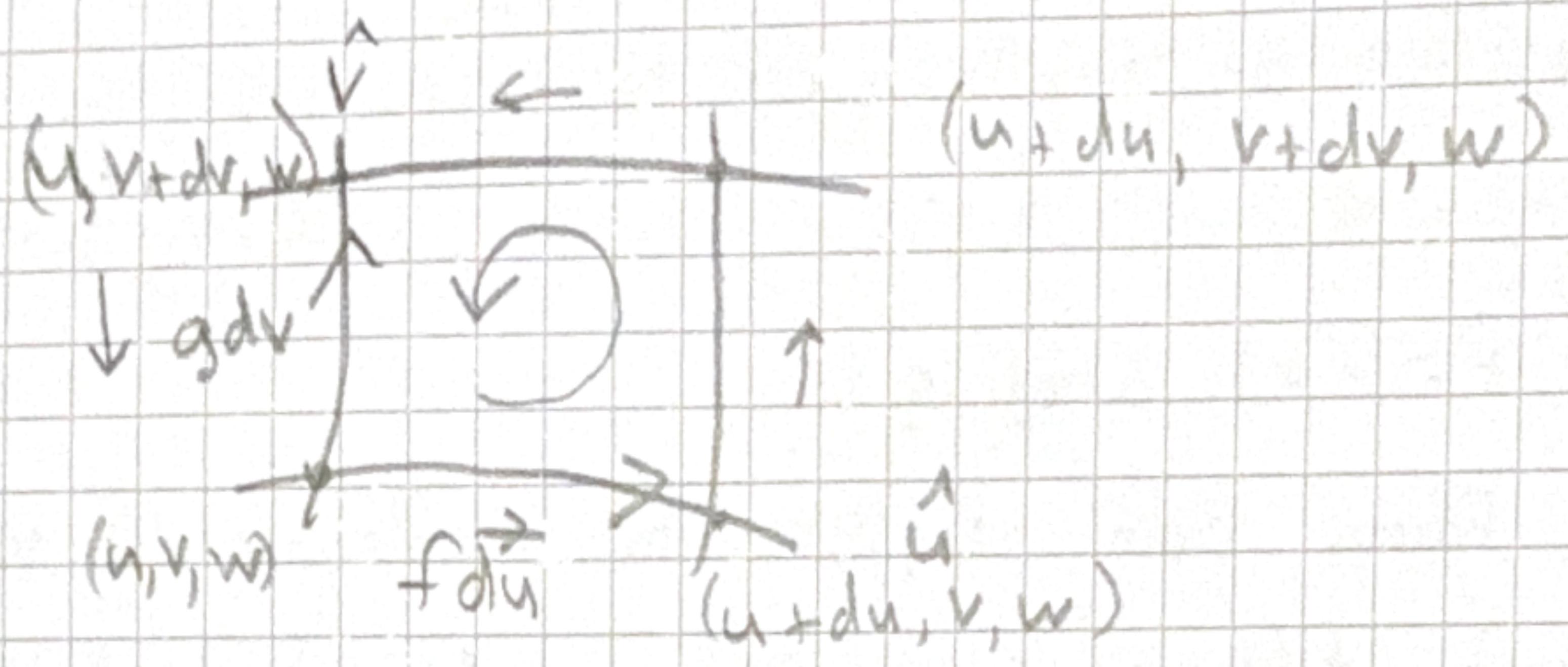
\(\hat{w}\) out of page \[ d \mathbf{a}=f g \text { dudv } \hat{w} \] along bottom segment \(d \mathbf{l}=f d u \hat{u}\) \[ \mathbf{A} \cdot d \mathbf{l}=\left(f A_{u}\right) d u \] along top leg A is evaluated at \(v+d v\) \[ \left(\left|-\left(f A_{u}\right)\right|_{v + d v}+\left.\left(f A_{u}\right)\right|_{v}\right) d u=-\left[\frac{\partial}{\partial v}\left(f A_{u}\right)\right] d u d v \] right and left hand sides give \[ \left[\frac{\partial}{\partial u}\left(g A_{v}\right)\right] d u d v \]

total is \[ \begin{aligned} \oint A \cdot d\mathbf{a} & =\left[\frac{\partial}{\partial u}\left(g A_{v}\right)-\frac{\partial}{\partial v}\left(f A_{u}\right)\right] d u dv \\ & =\frac{1}{fg}\left[\frac{\partial}{\partial u}\left(g A_{v}\right)-\frac{\partial}{\partial v}\left(f A_{u}\right)\right] \hat{w} \cdot d \mathbf{a} \end{aligned} \]

This provides the \(w\) component of curl.

If we then do the other directions (a general patch not just in the u-v plane) we will get: \[ \begin{aligned} \nabla \times \mathbf{A}=\frac{1}{g h} & \left[\frac{\partial}{\partial v}\left(h A_{w}\right)-\frac{\partial}{\partial w}\left(g A_{v}\right)\right] \hat{u}+\frac{1}{f h}\left[\frac { \partial } { \partial w } (f A_{u})-\frac{\partial}{\partial u}\left(h A_{w}\right)\right] \hat{v}\\ &+\frac{1}{f g}\left[\frac{\partial}{\partial u}(g A_v)-\frac{\partial}{\partial v}\left(f A_{u}\right)\right] \hat{w} \end{aligned} \]

12.4 Laplacian

Derive by using divergence and gradient in general form.

\[ \nabla^2 t = \frac{1}{fgh}\left[\frac{\partial}{\partial u}\left(\frac{gh}{f}\right)\frac{\partial t}{\partial u} + \frac{\partial}{\partial v}\left(\frac{fh}{g}\right)\frac{\partial t}{\partial v} + \frac{\partial}{\partial w}\left(\frac{fg}{h}\right)\frac{\partial t}{\partial w}\right] \]