11 Line Integrals
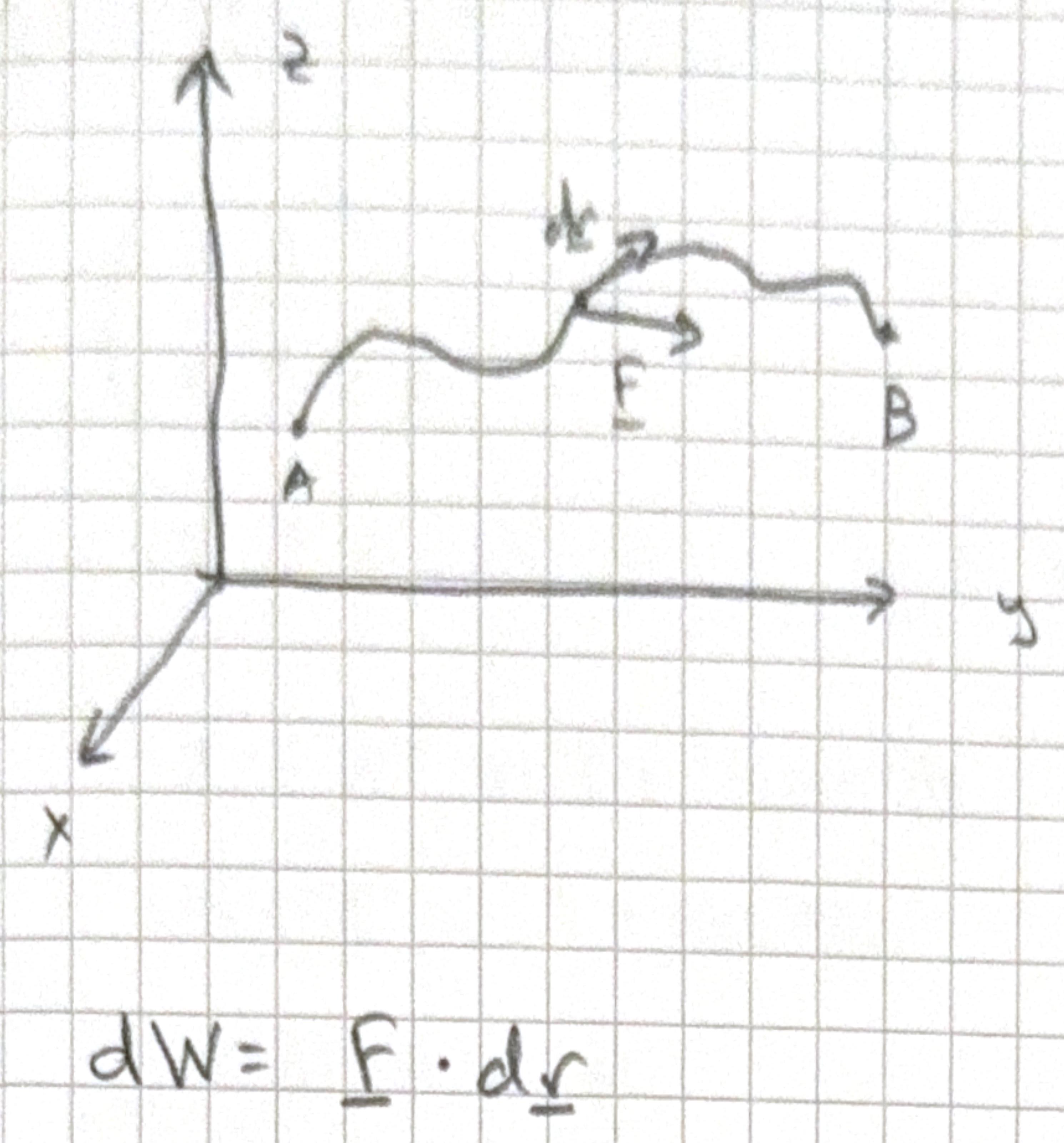
Lets say we have a charged particle in an electric field and we need to calculate the work needed for it to move from point \(A\) to \(B\) along a particular path. The coordinates \(x, y,+z\) are constrained by the equation of the path. The path is one dimensional and can be written in terms of one variable. The total work is the integral over the path and can be written in terms of the one independent variable either by writing two of the coordinates in terms of the other or by writing parametric equations. \[ \begin{aligned} & x=x_{0}+a s \\ & y=y_{0}+b s \\ & z=z_{0}+c s \end{aligned} \]
\[ \mathbf{F}=x y \hat{\imath}-y^{2} \hat{\jmath} \]
Find work done along the path \[ \begin{aligned} & d \mathbf{r}=\hat{\imath} d x+\hat{\jmath} d y \\ & \mathbf{F} \cdot d \mathbf{r}=x y d x-y^{2} d y \\ & W=\int_{\text {Path }} x y d x-y^{2} d y \end{aligned} \]
Write integrand interns of one variable
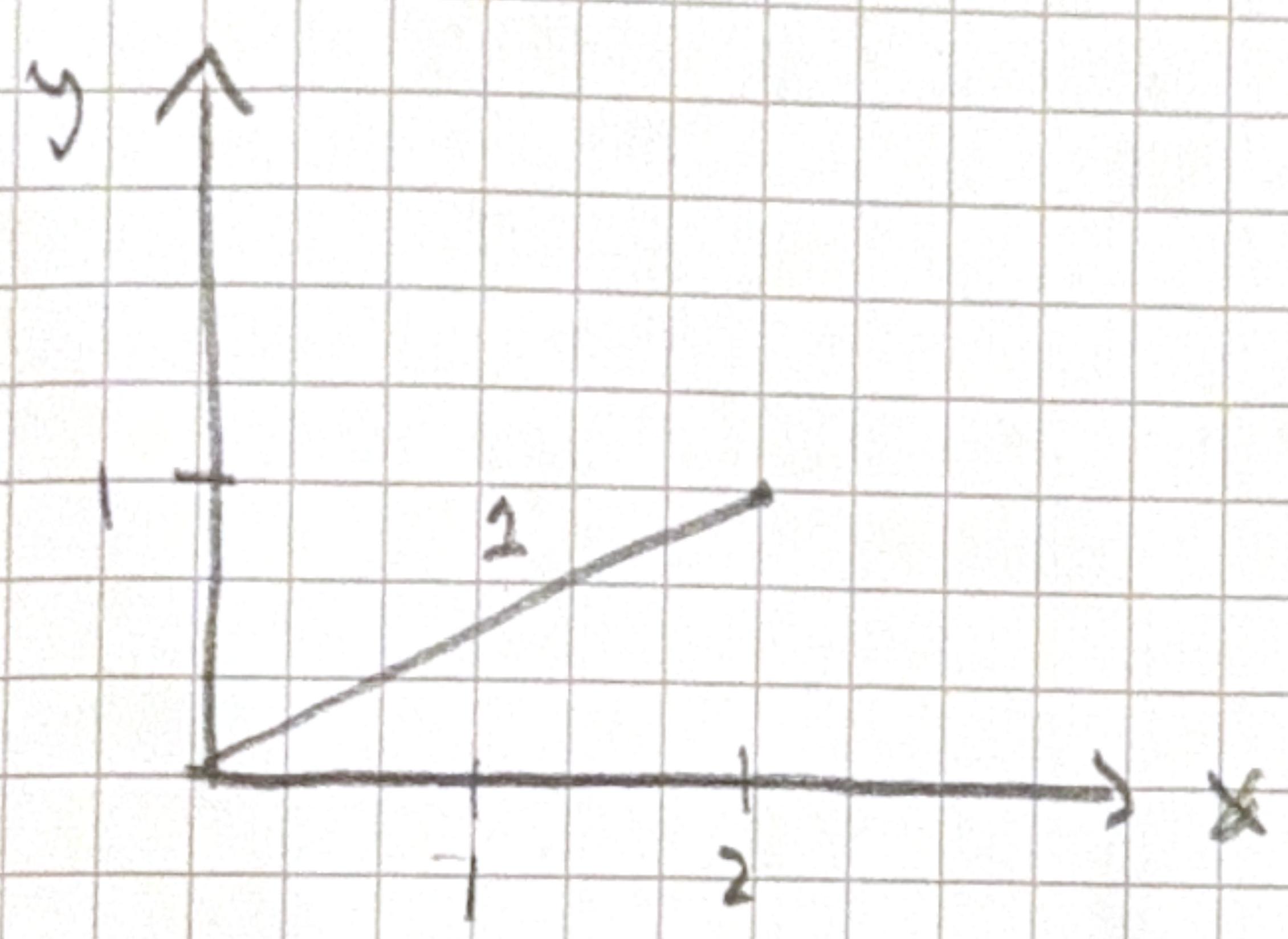
Lets start by taking path 1 a straight line \[ \begin{aligned} y & =1 / 2 x \\ d y & =1 / 2 d x \\ W & =\int_{0}^{2}\left(x \cdot \frac{1}{2} x- \frac{1}{4} x^{2} \cdot \frac{1}{2}\right) d x \\ & =\int_{0}^{2} \left(\frac{1}{2} x^{2}-\frac{1}{8} x^{2}\right) d x \\ & =\int_{0}^{2} \frac{3}{8} x^{2} d x \\ & =\left.\frac{1}{8} \cdot x^{3}\right|_{0} ^{2}=1 \end{aligned} \]
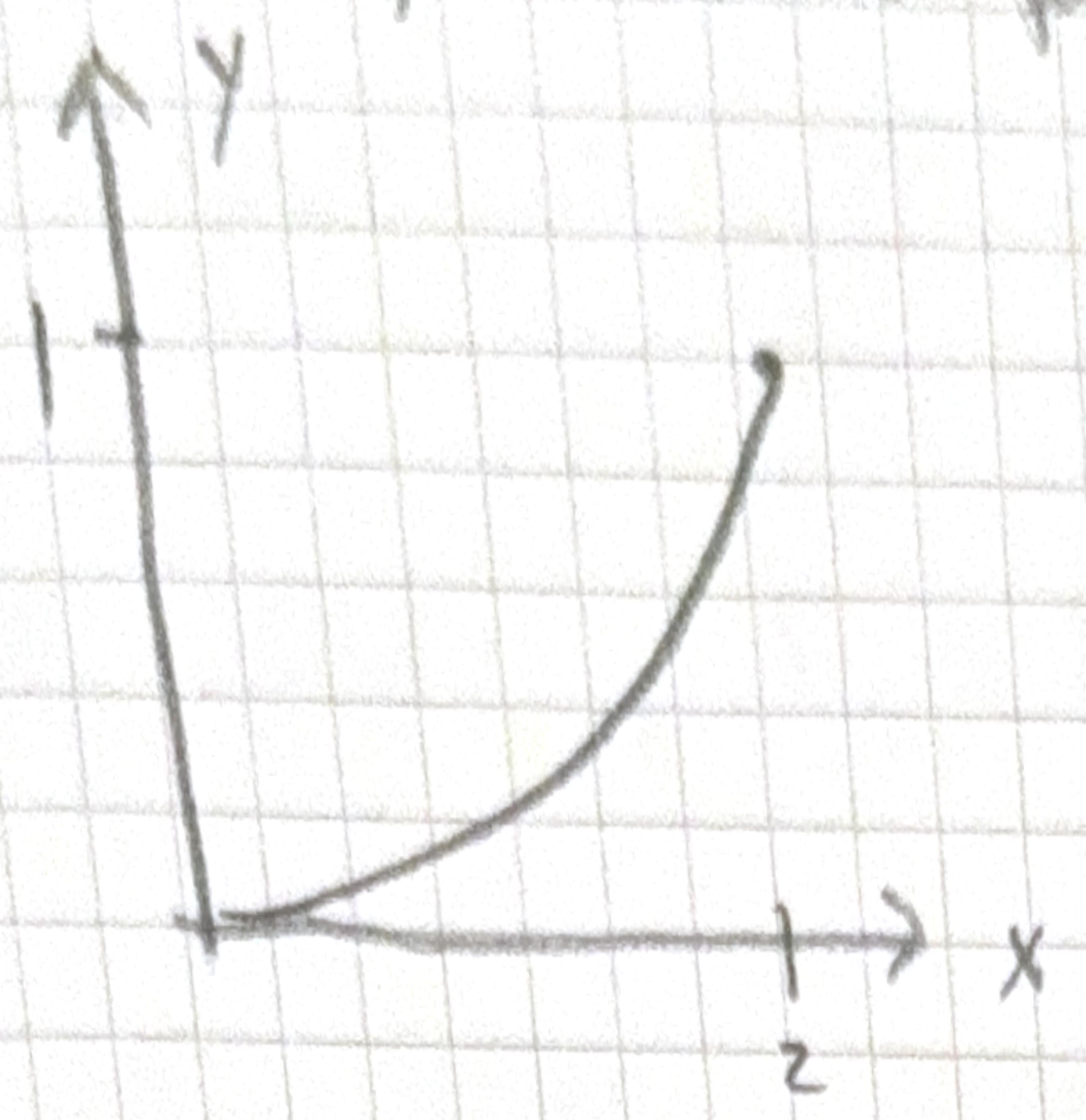
Now lets consider another path - a parabola
 \[
\begin{aligned}
y & =\frac{1}{4} x^{2} \quad d y=\frac{1}{2} x d x \\
W_{2} & =\int_{0}^{2} x \cdot \frac{1}{4} x^{2}-\frac{1}{16} x^{4} \cdot \frac{1}{2} x d x \\
& =\int_{0}^{2} \left( \frac{1}{4} x^{3}-\frac{1}{32} x^{5} \right) d x \\
& =\frac{x^{4}}{16}-\left.\frac{1}{192} x^{6}\right|_{0} ^{2} \\
& =1=\frac{64}{192}-\frac{2}{3}
\end{aligned}
\]
\[
\begin{aligned}
y & =\frac{1}{4} x^{2} \quad d y=\frac{1}{2} x d x \\
W_{2} & =\int_{0}^{2} x \cdot \frac{1}{4} x^{2}-\frac{1}{16} x^{4} \cdot \frac{1}{2} x d x \\
& =\int_{0}^{2} \left( \frac{1}{4} x^{3}-\frac{1}{32} x^{5} \right) d x \\
& =\frac{x^{4}}{16}-\left.\frac{1}{192} x^{6}\right|_{0} ^{2} \\
& =1=\frac{64}{192}-\frac{2}{3}
\end{aligned}
\]
The work calculated in the two paths is not the same. But there are several examples when it is (gravitational field for example). If the force field is path dependent it is a non-conservative force if it is path independent it is a conservative force.
A conservative force field means that \(\int \mathbf{F} \cdot d\mathbf{r}\) is the same no matter what path is taken.
Suppose \[ \begin{aligned} & \mathbf{F}=\nabla W \cdot d \mathbf{r} = \hat{\imath}\frac{\partial W}{\partial x}+\hat{\jmath}\frac{\partial W}{\partial y}+\hat{k} \frac{\partial W}{\partial z} \\ & F_{x}=\frac{\partial W}{\partial x}, \quad F_{y}=\frac{\partial W}{\partial y}, F_{z}=\frac{\partial W}{\partial z} \\ & \frac{\partial F_{x}}{\partial y}=\frac{\partial^{2} W}{\partial x \partial y}=\frac{\partial^{2} W}{\partial y \partial x}=\frac{\partial F_{y}}{\partial x} \end{aligned} \] similarly \[ \begin{aligned} & \quad \frac{\partial F_{z}}{\partial y}=\frac{\partial F_{y}}{\partial z} \text { and } \frac{\partial F_{x}}{\partial z}=\frac{\partial F_{z}}{\partial x} \\ & \therefore \nabla \times F=\mathbf{0} \end{aligned} \]
Thus if \(\mathbf{F}=\nabla W\) then \(\nabla \times \mathbf{F}=\mathbf{0}\) and it also turns out that the reverse is true as well – if \(\nabla \times \mathbf{F}=\mathbf{0}\) than there is a function \(W\) for which \(\mathbf{F}=\nabla W\).
Now if \[ \begin{aligned} \mathbf{F} \cdot d \mathbf{r}=\nabla W \cdot d r & =\frac{\partial W}{\partial x} d x+\frac{\partial W}{\partial y} d y+\frac{\partial W}{\partial z} d z \\ & =d W \end{aligned} \] and \[ \int_{A}^{B} \mathbf{F} \cdot d \mathbf{r}=\int_{A}^{B} d W=W(B)-W(A) \]
Where \(W(B)\) and \(W(A)\) mean the values of the function \(W\) at the end points \(A \& B\) of the path. Since the integral only depends on the end pants the integration is path independent and \(\mathbf{F}\) is a conservative field.
Just as we saw in problem 7 of week 3 problems the curl of the grad is always zero.