3 Differential Calculus
Suppose that we have a function of one variable \(f(x)\)
Q. What does the derivative \(\frac{d f}{d x}\) tell us?
Answer: It tells us how rapidly \(f(x)\) varies when we change \(x\) by a small amount \(d x\). \[ d f=\left(\frac{d f}{d x}\right) d x \] \(\frac{d f}{d x}\) is the slope of the graph of \(f\) versus \(x\)

\(\frac{d f}{d x}\) increases as we move away from the origin.
So what happens when a function depends on more than one variable? Lets take temperature in a room - \(T(x, y, z)\) ? \[ d T=\left(\frac{\partial T}{\partial x}\right) d x+\left(\frac{\partial T}{\partial y}\right) d y+\left(\frac{\partial T}{\partial z}\right) d z \]
\(dT\) describes mathematically how T varies when we chance all variables \(x, y\), and \(z\) a little bit \(d x, d y, d z\).
3.1 Gradient
We can rewrite the above as a dot product: \[ d T=\left(\frac{\partial T}{\partial x} \hat{x}+\frac{\partial T}{\partial y} \hat{y}+\frac{\partial T}{\partial z} \hat{z}\right) \cdot(d x \hat{x}+d y \hat{y}+d z \hat{z}) \] \[ \begin{aligned} & d T=\nabla T \cdot d \underline{l} \\ & \nabla T=\frac{\partial T}{\partial x} \hat{x}+\frac{\partial T}{\partial y} \hat{y}+\frac{\partial T}{\partial z} \hat{z} \end{aligned} \] \(\nabla T\) is called the gradient of \(T\) and is a vector quantity. Like any other vector \(\nabla T\) has both magnitude and direction. \[ d T=\nabla T \cdot d \underline{l}=|\nabla T||d \underline{l}| \cos \theta \] where \(\theta\) is the angle between \(\nabla\) and \(d l\).
- \(\nabla T\) points in the direction of maximum increase of the function \(T\).
- The magnitude of \(\nabla T\) is the slope along the maximal increase.
Find the gradient of \(r=\sqrt{x^{2}+y^{2}+z^{2}}\) (the magnitude of the position vector).
\[ \begin{aligned} & \nabla r=\frac{\partial}{\partial x} r \hat{x}+\frac{\partial}{\partial y} r \hat{y}+\frac{\partial}{\partial z} r \hat{z} \\ & \frac{\partial r}{\partial x}=\frac{1}{2}\left(x^{2}+y^{2}+z^{2}\right)^{-1 / 2} \cdot 2 x \\ & \frac{\partial r}{\partial y}=\frac{1}{2}\left(x^{2}+y^{2}+z^{2}\right)^{-1 / 2} \cdot 2 y \\ & \frac{\partial r}{\partial z}=\frac{1}{2}\left(x^{2}+y^{2}+z^{3}\right)^{-1 / 2} \cdot 2 z \\ & r=\left(x^{2}+y^{2}+z^{2}\right)^{1 / 2} \Rightarrow \frac{1}{r}=\left(x^{2}+y^{2}+z^{2}\right)^{-1 / 2} \\ & \therefore \nabla r=\frac{x \hat{x}+y \hat{y}+z \hat{z}}{\left(x^{2}+y^{2}+z^{2}\right)^{1 / 2}}=\frac{\hat{r}}{|r|}=\hat{r} \end{aligned} \]
We call \(\nabla\) del and it is a vector operator. Del acts somewhat like a normal vector and can “act” in three ways
- it can multiply a scalar. \(\Rightarrow\) gradient \(\nabla T\)
- it can be dotted with a vector \(\nabla \cdot \underline A \Rightarrow\) we call this divergence
- it can be “crossed” with a vector \(\nabla \times \underline A \Rightarrow\) this is called curl.
3.2 Divergence
\[ \begin{aligned} \nabla \cdot \underline{v} & =\left(\frac{\partial}{\partial x} \hat{x}+\frac{\partial}{\partial y} \hat{y}+\frac{\partial}{\partial z} \hat{z}\right) \cdot\left(v_{x} \hat{x}+v_{y} \hat{y}+v_{z} \hat{z}\right) \\ & =\frac{\partial}{\partial x} v_{x}+\frac{\partial}{\partial y} v_{y}+\frac{\partial}{\partial z} v_{z} \end{aligned} \]
The divergence of a vector is a scalar. It represents the spreading out of a vector from the point in question.
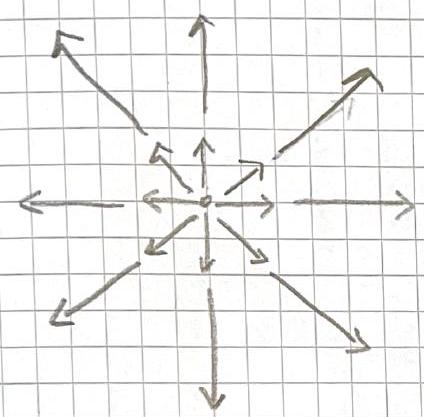


\[ v_{a}=x \hat{x}+y \hat{y}+z \hat{z}, v_{b}=\hat{z}, v_{c}=z \hat{z} \]
- \(\underline{\nabla} \cdot \underline{v}_{a}=\frac{\partial}{\partial x} x+\frac{\partial}{\partial y} y+\frac{\partial}{\partial z} z\) \(=3\) pos. divergence
- \(\underline{\nabla} \cdot \underline{v}_{b}=\frac{\partial}{\partial x}(0)+\frac{\partial}{\partial y}(0)+\frac{\partial}{\partial z}(1)=0\)
- \(\underline{\nabla} \cdot \underline{v}_{c}=\frac{\partial(0)}{\partial x}+\frac{\partial}{\partial y}(0)+\frac{\partial z}{\partial z}=1\) pos. divergence
3.3 The Curl
\[ \begin{aligned} \underline{\nabla} \times \underline{v} & =\left|\begin{array}{ccc} \hat{x} & \hat{y} & \hat{z} \\ \partial / \partial x & \partial / \partial y & \partial / \partial z \\ v_{x} & v_{y} & v_{z} \end{array}\right| \\ & =\hat{x}\left[\frac{\partial v_{z}}{\partial y}-\frac{\partial v_{y}}{\partial z}\right]-\hat{y}\left[\frac{\partial v_{z}}{\partial x}-\frac{\partial v_{x}}{\partial z}\right] \\ & +\hat{z}\left[\frac{\partial v_{y}}{\partial x}-\frac{\partial v_{x}}{\partial y}\right] \end{aligned} \]
- The curl of a vector is a vector
Geometric interpretation is how much a vector curls around the paint in question.
Previous figures \(\rightarrow\) have 0 curl above have non-zero curl.
\(\quad \mathbf{v}_{a}=-y \hat{x}+x \hat{y}, \quad \mathbf{v}_{b}=x \hat{y}\)
Calculate curl: \(\nabla \times \mathbf{v}_{a}\)
\(\nabla \times \mathbf{v}_{a}=\left|\begin{array}{ccc}\hat{x} & \hat{y} & \hat{z} \\ \partial / \partial x & \partial / \partial y & \partial / \partial z \\ -y & x & 0\end{array}\right|\)
\[ \begin{aligned} & =\hat{x}\left(\frac{\partial}{\partial y}(0)-\frac{\partial}{\partial z}(x)\right)-\hat{y}\left(\frac{\partial}{\partial x}(0)-\frac{\partial}{\partial z}(-y)\right) \\ & +\hat{z}\left(\frac{\partial}{\partial x} x-\frac{\partial}{\partial y}(-y)\right) \\ & =0 \hat{x}-0 \hat{y}+2 \hat{z} \end{aligned} \]
Calculate curl: \(\underline{\nabla} \times \mathbf{v}_{b}\)
\(\underline{\nabla} \times \mathbf{v}_{b}=\left|\begin{array}{ccc}\hat{x} & \hat{y} & \hat{z} \\ \partial / \partial x & \partial / \partial y & \partial / \partial z \\ 0 & x & 0\end{array}\right|\) \[ \begin{aligned} & =\hat{x}(\partial / \partial y(0)-\partial \partial \partial z(x))-\hat{y}(\partial / \partial x(0)-\partial \partial z(0))+\hat{z}(\partial \partial x(x)-\partial / \partial y(0)) \\ & =1 \hat{z} . \end{aligned} \]
3.4 The Laplacian
One can also take the divergence of a gradient of a scalar field: \(\nabla \cdot \nabla \phi\) or \(\nabla^2 \phi\) (the Laplacian of \(\phi\)).
\[ \begin{aligned} & \nabla^2 \phi = \frac{\partial}{\partial x}\frac{\partial \phi}{\partial x}+\frac{\partial}{\partial y}\frac{\partial \phi}{\partial y}+\frac{\partial}{\partial z}\frac{\partial \phi}{\partial z}\\ & = \frac{\partial^2 \phi}{\partial x^2}+\frac{\partial^2 \phi}{\partial y^2}+\frac{\partial^2 \phi}{\partial z^2} \end{aligned} \]