4 Line, Surface, and Volume Integrals
In electrodynamics you will encounter several different kinds of integrals such as line (path), surface (flux), and volume.
4.1 Line integrals
\[ \int_{a}^{b} \underline{v} \cdot d \underline{l} \] where \(\underline{v}\) is a vector function, \(d \underline{l}\) is an infinitesimal displacement vector and the integral is calculated a long a specific path \(P\) from a point \(a\) to a point \(b\).
If the path forms a closed loop meaning the end point is the same as the starting point \(a=b\) this is shown as a circle on the integral: \[ \oint_{a}^{b} \underline{v} \cdot d \underline{l} . \]
In order to calculate the path integral take the dot product of \(\underline{v}\) evaluated at that point with displacement \(d\) d to the next point on the path.
Think of an example of a path integral in physics?
Work: \(W=\int \underline{E} \cdot d \underline{l}\) Work done by a force \(\underline{E}\).
Note: A conservative force is a force that is independent of path.
Calculate the line integral of the function \(\mathbf{v} = y^{2} \hat{x}+2 x(y+1) \hat{y}\) form point \(a=(1,1,0)\) to point \(b=(2,2,0)\) along paths (1) and (2).
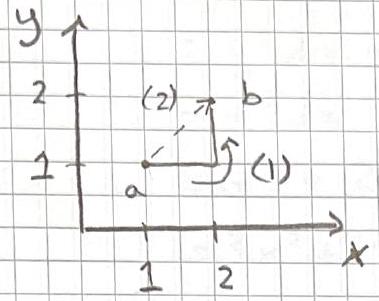
\[ d \underline{\ell}=d x\, \hat{x}+d y\, \hat{y}+d z\, \hat{z} \]
Path (1)
first part \(d y=d z=0\), \(d \underline{l}=d x \,\hat{x}\) and \(y=1\). \[ \begin{aligned} \underline{v} \cdot d \underline{l} & =y^{2} d x \, @ \, y=1 \\ & =d x \\ \int \underline{v} \cdot d \underline{l} & =\int_{1}^{2} d x=1 \end{aligned} \]
second part of Path 1 (the vertical part \(d\underline{l} = dy \, \hat y\) and \(x = 2\).) \[ \begin{aligned} \int \underline{v} \cdot d \underline{l}=\int_{1}^{2} 2 x(y+1) d y \\ & x=2 \\ & =\int_{1}^{2} 4(y+1) d y \\ & = \left. (2 y^{2}+ 4 y)\right|_{1} ^{2} \\ & =(8+8)-6=10 \text {. } \end{aligned} \]
So all together path 1: \(\int \underline{v} \cdot d \underline{l}=11\).
Path \(2: x=y \quad d x=d y\) and \(d z=0\). \[ \begin{aligned} & d \underline{\underline{l}}=d x\, \hat{x}+d y\, \hat{y} \\ & \underline{v} \cdot d \underline{l}=y^{2} d x+2 x(y+1) d y \end{aligned} \] but \(d x=d y\) and \(x=y\) \[ \begin{aligned} & =y^{2} d x+2 x(y+1) d x \\ & =x^{2} d x+2 x(x+1) d x \\ & =\left(x^{2}+2 x^{2}+2 x\right) d x \\ & =\left(3 x^{2}+2 x\right) d x \end{aligned} \] \[ \begin{aligned} \int \underline{v} \cdot d\underline{l} = & \int_{1}^{2}\left(3 x^{2}+2 x\right) d x=\frac{3 x^{3}}{3}+\left.\frac{2 x^{2}}{2}\right|_{1} ^{2} \\ & =x^{3}+\left.x^{2}\right|_{1} ^{2} \\ & =(8+4)-2=10 \\ \text { Path } 2 & =10 \end{aligned} \]
What is \(\oint \underline{v} \cdot d \underline{1}\) for the loop that goes from \(a\) to \(b\) out on path (1) and back on path (2)?
\[ \oint \underline{v} \cdot d \underline{l}=11-10=1 \]
4.2 Surface Integrals
\[ \int_{S} \underline{v} \cdot d \underline{a} \] where \(\underline{v}\) is a vector function and \(d\underline{a}\) is a little bit of area with direction perpendicular to the surface.
Similarly to the path integral \(\oint \underline{v} \cdot d \underline{a}\) indicates a closed surface.
Generally outward is positive for a surface but if the surface is open this is arbitrary. If \(\underline{v}\) describes flow then \(\int \underline{v} \cdot d \underline{a}\) is the total mas through the surface per unit time (or flux).
Calculate the surface integral of \[ v=2 x z \hat{x}+(x+2) \hat{y}+y(z^2-3) \hat{z} \] over five sides of a cubical box (excluding the bottom).
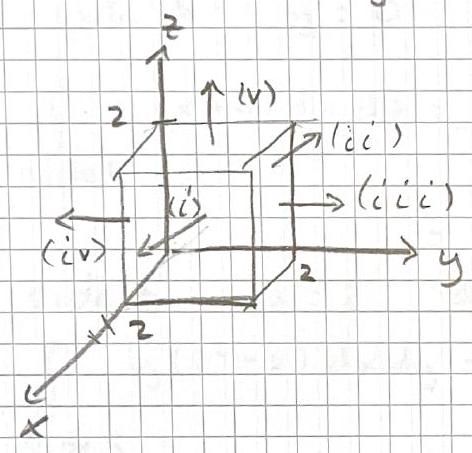
Let do one side at a time:
For side (i) \(x=2\) and \(d \underline{a}=d y d z \hat{x}\) \[ \begin{aligned} \int_{\text {side } 1} v \cdot d \underline{a} & =\int_{0}^{2} \int_{0}^{2} 2 x z \, dy \, dz \\ & =\int_{0}^{2} d y \int_{0}^{2} 4 z d z \\ & =\left.\left.y\right|_{0} ^{2} \cdot 2 z^{2}\right|_{0} ^{2} \\ & =2 \cdot 8=16 \end{aligned} \]
Side \(2 \quad x=0 \quad d \underline{a}=-d y \,d z \,\hat{x}\) \[ \int_{\text {side } 2} \underline{v} \cdot d \underline{a}=\int-2 x z \, d y \, d z=0 \]
Side \(3 \quad y=2 \quad d \underline{a}=d x \, d z \, \hat{y}\) \[ \begin{aligned} \int_{\text {side } 3}(x+2) \, d x \, d z & =\int_{0}^{2} d z \int_{0}^{2}(x+2) d x \\ & =\left.\left.z\right|_{0} ^{2} \cdot\left(\frac{x^{2}}{2}+2 x\right)\right|_{0} ^{2} \\ & =2 \cdot 6=12 \end{aligned} \]
Side \(4 \quad y=0 \quad d \underline{a}=-d x\, d z\, \hat{y}\) \[ \begin{aligned} \int_{\text {side } 4}-(x+2) d x d z & =-\int_{0}^{2} d z \int_{0}^{2}(x+2) d x \\ & =-12 \end{aligned} \]
Side \(5 \quad z=2 \quad d \underline{a}=d x \, d y \, \hat{z}\) \[ \begin{aligned} & \int_{\text {Side } 5} y\left(z^{2}-3\right) d x d y=\int_{0}^{2} d x \int_{0}^{2} y \, d y \\ &=\left.2 \cdot \frac{y^{2}}{2}\right|_{0} ^{2} \\ &=4 \\ & \therefore \int_{S} \underline{v} \cdot d \underline{a}=16+0+12-12+4=20 . \end{aligned} \]
4.3 Volume Intugrals
\[ \int_{V} T d \tau \]
Where \(T\) is a scalar function and \(d \tau\) is a small volume element. \[ d \tau=d x d y d z \]
If \(T\) is the density of something that might vary from point to point the volume integral would give the total mass.
Calculate the volume integral of \(T=x y z^{2}\) over the prism
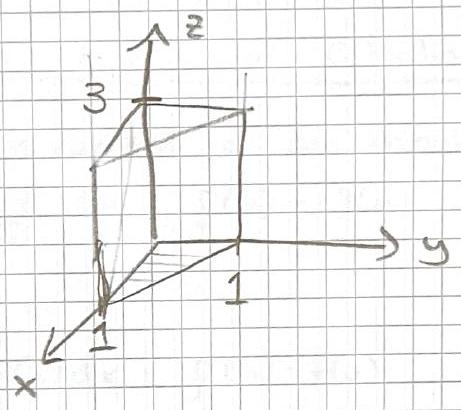
\[ \begin{aligned} \int_{V} T d \tau & =\int_{0} x y z^{2} d x d y d z \\ & =\int_{0}^{3} \int_{0}^{1} \int_{0}^{1-y} x y z^{2} d x d y d z \\ & =\left. \int_{0}^{3} \int_{0}^{1} \frac{x^{2}}{2} y z^{2}\right|_{0} ^{1-y} d y d z \\ & =\int_{0}^{3} z^{2} d z \int_{0}^{1} \frac{(1-y)^{2}}{2} y \,d y \end{aligned} \] \[ \begin{aligned} & =\left.\frac{z^{3}}{3}\right|_{0} ^{3} \cdot \int_{0}^{1} y\frac{(1-2 y+y^{2})}{2} d y \\ & =\frac{9}{2} \int_{0}^{1}\left(y-2 y^{2}+y^{3}\right) d y \\ & =\left.\frac{9}{2}\left(\frac{y^{2}}{2}+\frac{2}{3} y^{3}+\frac{y^{4}}{4}\right)\right|_{0} ^{1} \\ & =\frac{9}{2}\left(\frac{1}{2}-\frac{2}{3}+\frac{1}{4}\right) \\ & =\frac{9}{2}\left(\frac{6-8+3}{12}\right) \\ & =\frac{9}{2} \cdot \frac{1}{12}=\frac{3}{8} \end{aligned} \]