14  Spherical Coordinates

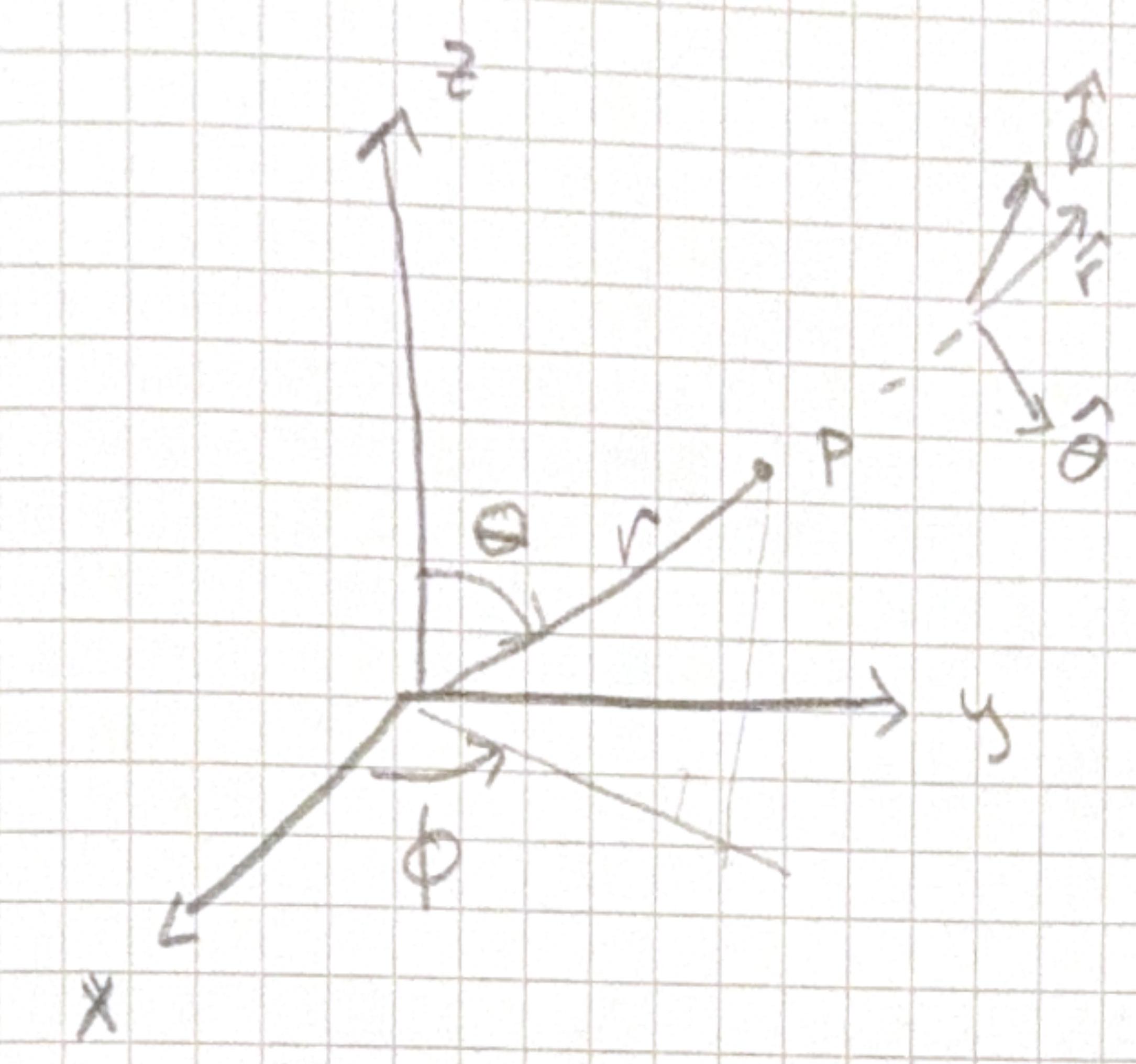
\(P\) is defined by \(r, \theta, \phi\) in spherical coordinates. \(r\) is the distance from the origin

\(\theta\) is the angle down from \(z\)-axis

\(\phi\) is the angle around \(z\) - axis (same as cylindrical coords) \[ x=r \sin \theta \cos \phi, \quad y=r \sin \theta \sin \phi, \quad z=r \cos \theta \] the unit vectors \(\hat{r}, \hat{\theta}, \hat{\phi}\) are mutually orthogonal \[ \mathbf{A}=A_{r} \hat{r}+A_{\theta} \hat{\theta}+A_{\phi} \hat{\phi} \]

\[ \begin{aligned} & d l_{r}=d r \\ & d l_{\theta}=r d \theta \\ & d l_{\phi}=r \sin \theta d \phi \end{aligned} \] arc lengths for angles must be converted into lengths \[ \begin{aligned} & d \mathbf{l}=d r \hat{r}+r d \theta \hat{\theta}+r \sin \theta d \phi \hat{\phi} \\ & d \tau=d l_r d l_{\theta} d l_\phi=r^{2} \sin \theta d r d \theta d \phi \end{aligned} \] r ranges from 0 to \(\infty, \theta\) from \(0\) to \(\pi\), \(\phi\) from \(0\) to \(2 \pi\)

Lets just think a bit about area

Question

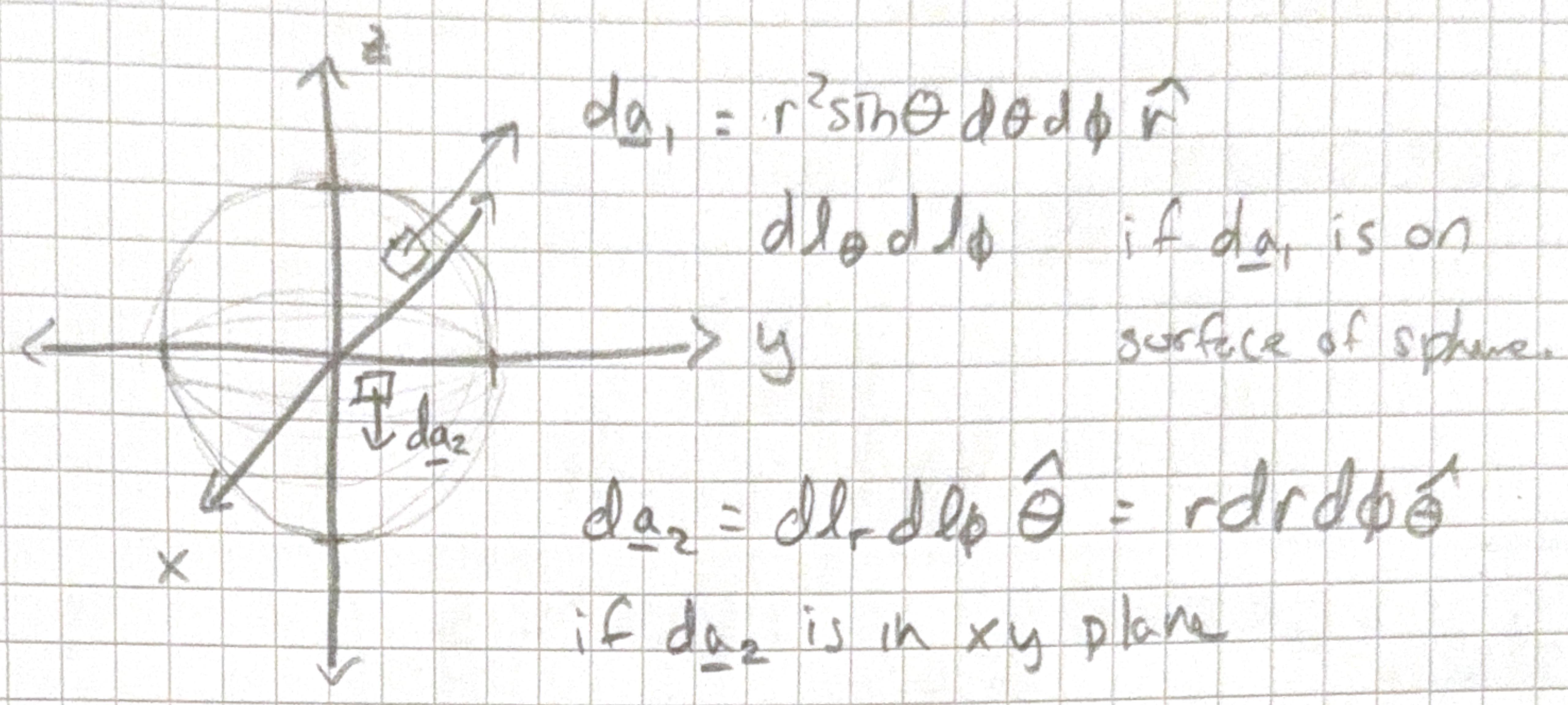
Find volume of a sphere of radius \(R\).

Answer

\[ \begin{aligned} V=\int d \tau & =\int_{r=0}^{R} \int_{\theta=0}^{\pi} \int_{\phi=0}^{2 \pi} r^{2} \sin \theta d \phi d \theta d r \\ & =\int_{0}^{R} r^{2} d r \int_{0}^{\pi} \sin \theta d \theta \int_{0}^{2 \pi} d \phi \\ & =\left.\left.\left.\frac{r^{3}}{3}\right|_{0} ^{R} \cdot -\cos \theta\right|_{0} ^{\pi} \cdot \phi\right|_{0} ^{2 \pi} \\ & =\frac{R^{3}}{3} 2 \cdot 2 \pi \\ V & =\frac{4}{3} \pi R^{3} \end{aligned} \]

Now lets use the general expressions to find the \(\nabla\) operators for spherical coordinates. \[ \begin{aligned} & \nabla t_{u}=\frac{1}{f} \frac{\partial t}{\partial u}, \nabla t_{v}=\frac{1}{g} \frac{\partial t}{\partial v}, \nabla t_{w}=\frac{1}{h} \frac{\partial t}{\partial w} \\ & d \underline{l}=f d u \hat{u}+g d v \hat{v}+h d w \hat{w} \\ & f=1, g=r, h=r \sin \theta \\ & \nabla T=\frac{\partial T}{\partial r} \hat{r}+\frac{1}{r} \frac{\partial T}{\partial \theta} \hat{\theta}+\frac{1}{r \sin \theta} \frac{\partial T}{\partial \phi} \hat{\phi} \end{aligned} \]

Divergence: \[ \begin{aligned} \nabla \cdot \mathbf{A} &= \frac{1}{fgh}\left[\frac{\partial}{\partial u}(gh A_u) + \frac{\partial}{\partial v} + (fh A_v)\frac{\partial}{\partial w}(fg A_w) \right]\\ &= \frac{1}{r^2 \sin \theta}\left[\frac{\partial}{\partial r} (r^2 \sin \theta A_r) + \frac{\partial}{\partial \theta} (r \sin \theta A_\theta) + \frac{\partial}{\partial \phi} (r A_\phi)\right]\\ \nabla \cdot \mathbf{A} &= \frac{1}{r^2}\frac{\partial}{\partial r} (r^2 A_r) + \frac{1}{r \sin \theta}\frac{\partial}{\partial \theta} (r \sin \theta A_\theta) + \frac{1}{r \sin \theta}\frac{\partial}{\partial \phi} (r A_\phi) \end{aligned} \]

Curl: \[ \begin{aligned} \nabla \times \mathbf{A} &= \frac{1}{g h}\left[\frac{\partial}{\partial v}\left(h A_{w}\right)-\frac{\partial}{\partial w}\left(gA_{v}\right)\right]\hat{u} \\ & +\frac{1}{f h}\left[\frac{\partial}{\partial w}(f A_u)-\frac{\partial}{\partial u}(h A_w)\right]\hat{v} \\ & +\frac{1}{f g}\left[\frac{\partial}{\partial u}(g A_v)-\frac{\partial}{\partial v}\left(f A_{u}\right)\right] \hat{w} \\ & =\frac{1}{r^{2} \sin \theta}\left[\frac{\partial}{\partial \theta}(r \sin \theta A_\phi)-\frac{\partial}{\partial \phi}(r A_\theta)\right] \hat{r} \\ & +\frac{1}{r \sin \theta}\left[\frac{\partial}{\partial \phi} A_{r}-\frac{\partial}{\partial r} (\sin \theta A_{\phi})\right]\hat{\theta} \\ & +\frac{1}{r}\left[\frac{\partial}{\partial r}\left(r A_{\theta}\right)-\frac{\partial}{\partial \theta}A_r\right]\hat{\phi} \\ & =\frac{1}{r \sin \theta}\left[\frac{\partial}{\partial \theta}(\sin \theta A_\phi)-\frac{\partial}{\partial \phi}(A_\theta)\right] \hat{r} \\ & +\frac{1}{r}\left[\frac{1}{\sin \theta}\frac{\partial}{\partial \phi} A_{r}-\frac{\partial}{\partial r} (A_{\phi})\right]\hat{\theta} \\ & +\frac{1}{r}\left[\frac{\partial}{\partial r}\left(r A_{\theta}\right)-\frac{\partial}{\partial \theta}A_r\right]\hat{\phi} \end{aligned} \]

Laplacian: \[ \begin{aligned} \nabla^2 t &= \frac{1}{fgh}\left[\frac{\partial}{\partial u}\left(\frac{gh}{f}\right)\frac{\partial t}{\partial u} + \frac{\partial}{\partial v}\left(\frac{fh}{g}\right)\frac{\partial t}{\partial v} + \frac{\partial}{\partial w}\left(\frac{fg}{h}\right)\frac{\partial t}{\partial w}\right]\\ \nabla^2 t&= \frac{1}{r^2}\frac{\partial}{\partial r}\left(r^2\frac{\partial t}{\partial r}\right)+ \frac{1}{r^2 \sin \theta}\frac{\partial}{\partial \theta}\left(\sin \theta \frac{\partial t}{\partial \theta}\right) + \frac{1}{r^2 \sin^2 \theta}\left(\frac{\partial^2 t}{\partial \phi^2}\right) \end{aligned} \]

Question

Compute div of \[ \underline{v}=(r \cos \theta) \hat{r}+(r \sin \theta) \hat{\theta}+(r \sin \theta \cos \phi) \hat{\phi} \]

Answer

\[ \begin{aligned} \nabla \cdot \underline{v}= & \frac{1}{r^{2}} \frac{\partial}{\partial r}\left(r^{2} v_{r}\right)+\frac{1}{r \sin \theta} \frac{\partial}{\partial \theta}\left(\sin \theta v_{\theta}\right)+\frac{1}{r \sin \theta} \frac{\partial v_{\phi}}{\partial \phi} \\ = & \frac{1}{r^{2}} \frac{\partial}{\partial r} r^{3} \cos \theta+\frac{1}{r \sin \theta} \frac{\partial}{\partial \theta}(\sin \theta \cdot r \sin \theta) \\ & +\frac{1}{r \sin \theta} \frac{\partial}{\partial \phi}(r \sin \theta \cos \phi) \\ = & \frac{1}{r^{2}} 3 r^{2} \cos \theta+\frac{r}{r \sin \theta} 2 \sin \theta \cdot \cos \theta \\ & + \frac{1}{r \sin \theta} r \sin \theta \cdot-\sin \phi\\ = &3 \cos \theta+2 \cos \theta-\sin \phi\\ =& 5 \cos \theta-\sin \phi \end{aligned} \]

Question

Now check divergence theorem for this function using an inverted hemisphere of radius \(R\) as the volume and surface

Answer

Div theorem \[ \int_{V}(\nabla \cdot \underline{v}) d \tau=\oint_{S} \underline{v} \cdot d \underline{a} \] Left side first: \[ \begin{aligned} & \int_{0}^{2 \pi} \int_{0}^{\pi / 2} \int_{0}^{R}(5 \cos \theta-\sin \phi) r^{2} \sin \theta d r d \theta d \phi \\ & \int_{0}^{R} r^{2} d r \int_{0}^{\pi / 2} \int_{0}^{2 \pi}(5 \cos \theta-\sin \phi) \sin \theta d \phi d \theta \\ & \left.\int_{0}^{R} \frac{r^{3}}{3}\right|_{0} ^{R} \int_{0}^{\pi / 2} 5 \phi \cos \theta+\left.\cos \phi\right|_{\phi = 0} ^{2 \pi} \sin \theta d \theta \\ & \frac{R^{3}}{3} \int_{0}^{\pi / 2}[5 \cdot 2 \pi \cos \theta+(1-1)] \sin \theta d \theta \\ & \frac{R^{3}}{3} \int_{0}^{\pi / 2} 10 \pi \cos \theta \sin \theta d \theta \end{aligned} \] let \(u = \sin \theta\) \[ \begin{aligned} & d u=\cos \theta d \theta \\ & \frac{R^{3}}{3} \int 10 \pi u d u \\ & \left.\frac{R^{3}}{3} \cdot 10 \pi \frac{u^{2}}{2}\right|_{\theta=0} ^{\theta=\pi / 2} \\ & \left.\frac{R^{3}}{3} \cdot 10 \pi \frac{\sin ^{2} \theta}{2}\right|_{0} ^{\pi / 2} \\ & \frac{R^{3}}{3} \cdot 10 \pi \cdot \frac{1}{2}=\frac{5 \pi R^{3}}{3} . \end{aligned} \] Right side: Two surfaces - hemisphere and bottom

Start with hemisphere

\(\hat{r}\) component from \(\underline{v} \quad r=R\) \[ \begin{aligned} \int \underline{v} \cdot d \underline{a} & =\iint R \cos \theta \cdot R^{2} \sin \theta d \theta d \phi \\ & =R^{3} \int_{0}^{2 \pi} d \phi \int_{0}^{\pi / 2} \cos \theta \sin \theta d \theta \end{aligned} \] \[ \begin{aligned} u & =\sin \theta \\ d u & =\cos \theta d \theta \\ & =\left.R^{3} \cdot 2 \pi \cdot \frac{u^{2}}{2}\right|_{\theta=0} ^{\theta=\pi / 2} \\ & =\left.2 \pi R^{3} \cdot \frac{\sin ^{2} \theta}{2}\right|_{0} ^{\pi / 2} \\ & =\pi R^{3} \end{aligned} \]

Flat bottom \[ \begin{aligned} d \underline{a} & =r \sin \theta d r d \phi \hat{\theta} \quad \theta=\pi / 2\\ \int \underline{v} \cdot d \underline{a} & =\int_{0}^{2 \pi} \int_{0}^{R} r \sin \theta \cdot r \sin \theta d r d \phi \\ & =2 \pi \cdot \int_{0}^{R} r^{2} d r=\left.2 \pi \cdot \frac{r^{3}}{3}\right|_{0} ^{R} \\ & =\frac{2 \pi}{3} R^{3} \quad \therefore \text { Total }=\frac{5 \pi}{3} R^{3} \end{aligned} \]