2 Review of Vectors

Consider this situation: Walk 4 miles north and then 3 miles east (see Figure 2.1). How far have you walked?

7 miles - but you are not 7 miles from your starting point.

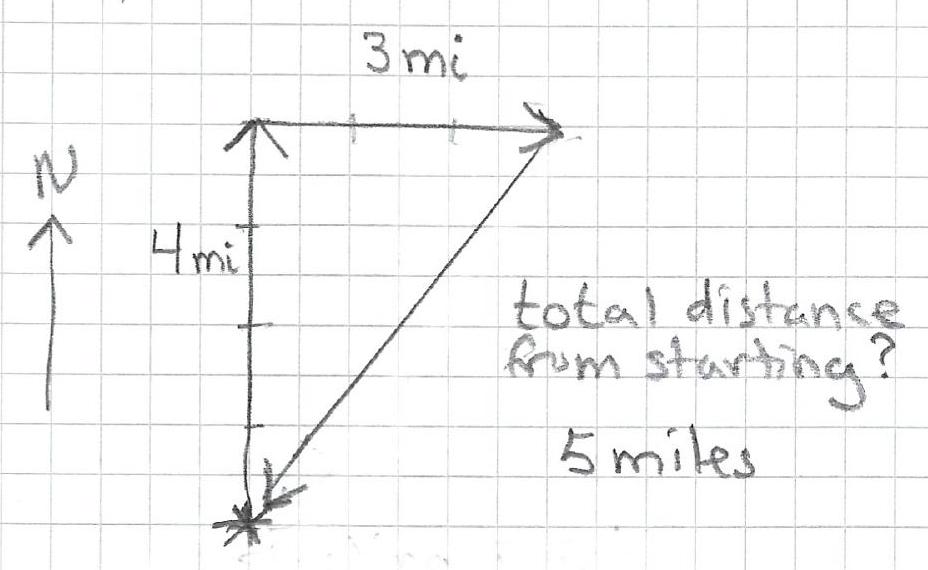
These quantities do not add in the standard way that we think of as addition because the displacements have direction as well as magnitude (length). Both the direction and the magnitude need to be taken into account When the quantities are combined. We also need a word for these quantities that have both magnitude and direction vectors.

Question

What are some examples of vector quantities that you often encounter in physics?

Answer

Velocity, acceleration, momentum, force…

However, not all quantities are vectors. Some quantities that we encounter in physics do not have direction. These quantities are scalars.

Question

What are some examples of scalar quantities that you often encounter in physics?

Answer

Mass, charge, density, temperature.

Vectors are identified in a number of ways - they can have a line under them or an arrow above or they many be in bold face: $\underline{A}$ or $\vec{A}$ or $\mathbf{A}$.

Scalars are not bold or can be specifically identified as the magnitude of a vector: $|A|$ or $A$.

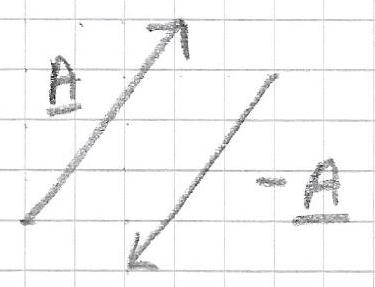
A negative sign in front of a vector, $- \vec{A}$, means that the vector points in a direction opposite to $\vec{A}$ but has the same magnitude (see Figure 2.2).

2.1 Vector Operations

Vectors do not have location - a displacement of 10 mi north from Bristol is represented by the same vector as a displacement 10 miles north from New York City. On a diagram you can slide the arrow around as long as it has the same length and direction that it did originally.

Addition of two vectors: \[ \underline{A}+\underline{B}=\underline{B}+\underline{A} \] 3 miles east then 4 miles north gets you to the same place as 4 miles north and then 3 miles east.

Vector addition is associative: \[ (\underline{A}+\underline{B})+\underline{C}=\underline{A}+(\underline{B}+\underline{C}). \]
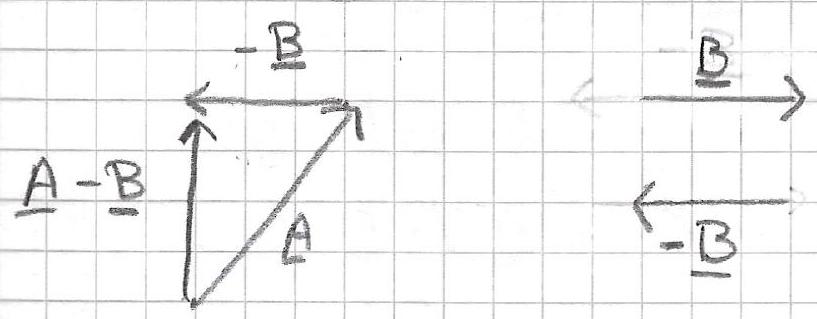
To subtract a vector you add its opposite: \[ \underline{A}-\underline{B}=\underline{A}+(-\underline{B}) \]

Multiplication of a vector by a scalar: \[a(\underline{A}+\underline{B})=a \underline{A}+a \underline{B}\] Multiplication of a vector by a positive scalar multiplies the magnitude but leaves the direction. If the scalar is negative the direction of the vector is reversed.
Dot product of two vectors: \[\underline{A} \cdot \underline{B}=A B \cos \theta ,\] where $\theta$ is the angle between $\underline{A}$ and $\underline{B}$ when they are placed tail to tail.

The dot product is a scalar (also called the scalar product).
The dot product is commutative, \[ \underline{A} \cdot \underline{B}=\underline{B} \cdot \underline{A}. \]
The dot product is distributive, \[ \underline{A} \cdot(\underline{B}+\underline{C})=\underline{A} \cdot \underline{B}+\underline{A} \cdot \underline{C}. \]

Question

What happens if $\underline{A}$ is parallel to $\underline{B}$?

Answer

\[\begin{aligned} \underline{A} \cdot \underline{B}=A B \cos \theta \\ \theta=0^{\circ} \\ \cos \theta=\cos 0^{\circ}=1 \\ \therefore \quad A \cdot \underline{B}=A B. \end{aligned}\]

Question

What happens to the dot product if $\underline{A}$ is perpendicular to $\underline{B}$?

Answer

\[ \begin{aligned} & \underline{A} \cdot \underline{B}=A B \cos \theta \\ & \text { If } A \perp B \text { then } \theta=90^{\circ} \\ & \cos 90^{\circ}=0\\ & \therefore \underline{A} \cdot \underline{B}=0. \end{aligned} \]

Question

Let $\underline{C}=\underline{A}-\underline{B}$. Calculate $\underline{C}\cdot\underline{C}$.

Answer

\[ \begin{aligned} \underline{C} \cdot \underline{C} & =(\underline{A}-\underline{B}) \cdot(\underline{A}-\underline{B}) \\ & =\underline{A} \cdot A - \underline{A} \cdot \underline{B} - \underline{B} \cdot \underline{A} + \underline{B} \cdot \underline{B} \\ & =A^{2}+B^{2}-2 \underline{A} \cdot \underline{B} \\ \underline{C}-\underline{C} & =A^{2}+B^{2}-2 A B \cos \theta \\ & \underline{C} \cdot \underline{C}=A^{2}+B^{2}-2 A B \cos \theta \end{aligned} \] This is the Law of Cosines

Cross Product of two vectors \[ \underline{A} \times \underline{B}=A B \sin \theta \,\hat{n}, \] where $\hat{n}$ is the unit vector (vector of length 1) pointing perpendicular to the plane defined by vectors $\underline{A}$ and $\underline{B}$. Note - the direction of $\hat{n}$ is ambiguous because there are two directions for this plane. It is resolved using right hand rule. Fingers point in direction of first vector and curl toward the second (smaller of two possible angles). The thumb then pants in direction of $\hat{n}$.

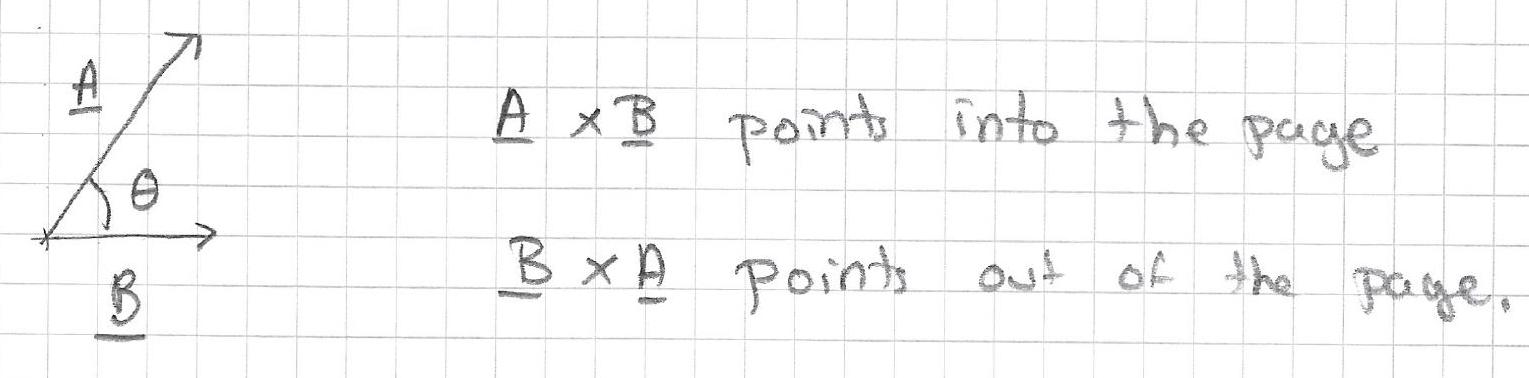
$\underline{A} \times \underline{B}$ is a vector.
The cross product is also called the vector product.
The cross product is distributive: \[ \underline{A} \times(\underline{B}+\underline{C})=\underline{A} \times \underline{B}+\underline{A} \times \underline{C} . \]
The cross produce is not commutative, \[ \underline{B} \times \underline{A}=-\underline{A} \times \underline{B} . \]
Geometrically $\underline{A} \times \underline{B}$ is the area of the parallelogram formed by $\underline{A}$ and $\underline{B}$.

Question

What is the cross product of two parallel vectors?

Answer

$\underline{A} \times \underline{A}=0$.

2.2 Vector Algebra

We have defined the vector function in abstract form but it is also possible to set up coordinates and work with vector components. Lets consider Cartesian coordinates - set up unit vectors $\hat{x}, \hat{y}, \hat{z}$ parallel to $x, y, z$ axes.

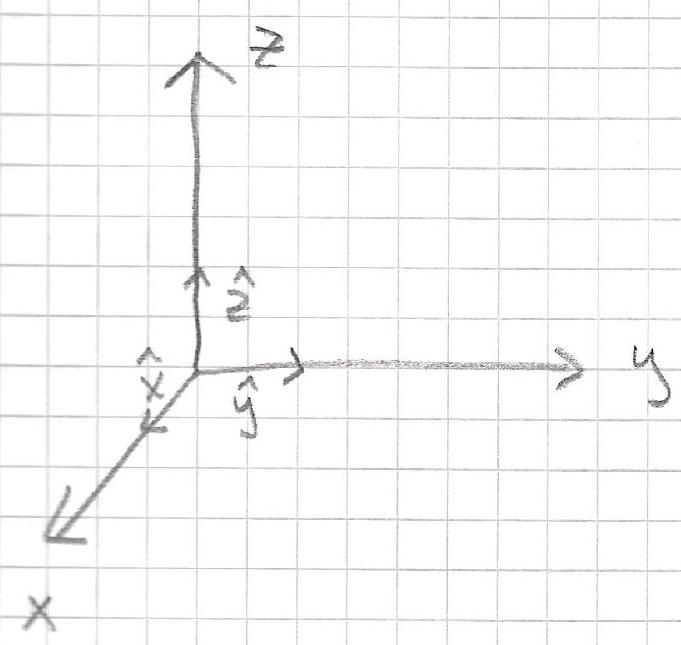
\[ \underline{A}=A_{x} \hat{x}+A_{y} \hat{y}+A_{z} \hat{z} \]

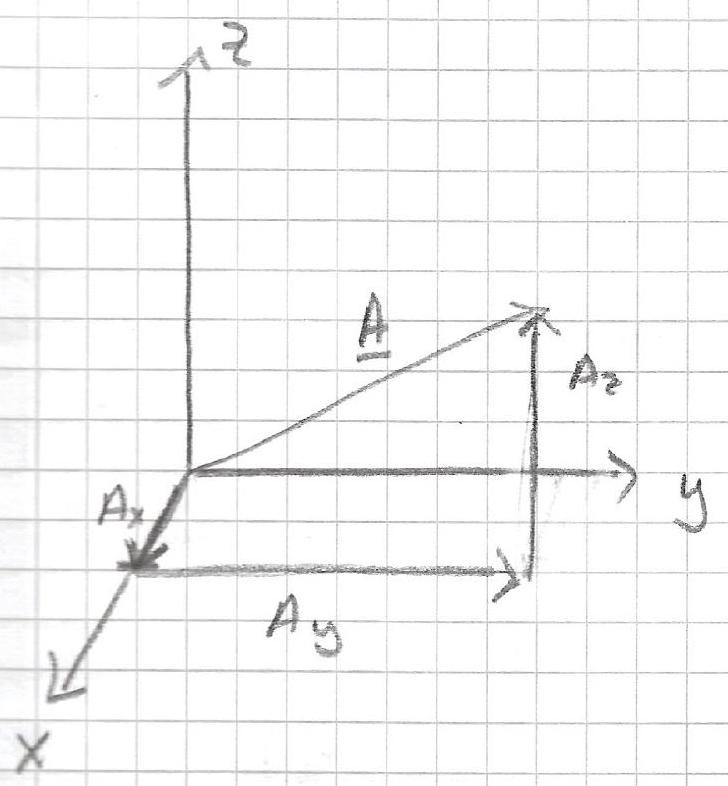
$A_{x}, A_{y}, A_{z}$ are projections of $\underline{A}$ along the respective coordinate axis.

Now lets return to the four vector functions that we covered earlier.

Vector addition: \[ \begin{aligned} \underline{A}+\underline{B} & =\left(A_{x} \hat{x}+A_{y} \hat{y}+A_{z} \hat{z}\right)+\left(B_{x} \hat{x}+B_{y} \hat{y}+B_{z} \hat{z}\right) \\ & =\left(A_{x}+B_{x}\right) \hat{x}+\left(A_{y}+B_{y}\right) \hat{y}+\left(A_{z}+B_{z}\right) \hat{z} \end{aligned} \] To add vectors in this form add components.
Scalar multiplication: \[ a \underline{A}=a A_{x} \hat{x}+a A_{y} \hat{y}+a_{z} \hat{z}\] To multiply by a scalar multiply each component by the scalar.
Dot product: \[ \begin{aligned} \underline{A} \cdot \underline{B} & =\left(A_{x} \hat{x}+A_{y} \hat{y}+A_{z} \hat{z}\right) \cdot\left(B_{x} \hat{x}+B_{y} \hat{y}+B_{z} \hat{z}\right). \\ & =A_{x} B_{x}+A_{y} B_{y}+A_{z} B_{z} \end{aligned} \] Note that since $\hat{x}, \hat{y}, \hat{z}$ are all mutually $\perp$ $\hat{x} \cdot \hat{x}=\hat{y} \cdot \hat{y}=\hat{z} \cdot \hat{z}=1$ and $\hat{x} \cdot \hat{y}=\hat{x} \cdot \hat{z}=\hat{y} \cdot \hat{z}=0.$ Thus, to calculate dot product multiply like components and add.

Question

Calculate $\underline{A} \cdot \underline{A}$.

Answer

$$ =A_{x}^{2}+A_{y}{2}+A_{z}^{2}

\[ A=\sqrt{A_{x}^{2}+A_{y}^{2}+A_{z}^{2}} \] magnitude of $A$.

Cross product: \[\underline{A} \times \underline{B}=\left(A_{x} \hat{x}+A_{y} \hat{y}+A_{z} \hat{z}\right) \times\left(B_{x} \hat{x}+ B_{y} \hat{y}+B_{z} \hat{z}\right). \]

You can multiply it all out and it will give you: \[ \begin{aligned} = \left(A_{y} B_{z}-A_{z} B_{y}\right) \hat{x}+\left(A_{z} B_{x}-A_{x} B_{z}\right) \hat{y} +\left(A_{x} B_{y}-A_{y} B_{x}\right) \hat{z}. \end{aligned} \]

Because $\hat{x} \times \hat{x}=\hat{y} \times \hat{y}=\hat{z} \times \hat{z}=0$ and \[ \left. \begin{array}{l} \hat{x} \times \hat{y}=-\hat{y} \times \hat{x}=\hat{z} \\ \hat{y} \times \hat{z}=-\hat{z} \times \hat{y} = \hat{x} \\ \hat{z} \times \hat{x}=-\hat{x} \times \hat{z}=\hat{y} \\ \end{array} \quad \right\} \text{ using right hand rule} \]

But there is an easier way to remember this:

\[A \times B=\left|\begin{array}{ccc}\hat{x} & \hat{y} & \hat{z} \\ A_x & A_y & A_z \\ B_x & B_y & B_z\end{array}\right| = \hat{x}\left(A_y B_z-A_z B_y\right)-\hat{y}\left(A_x B_z-A_z\right) +\hat{z}\left(A_x B_y-A_y B_x\right)\]

Question

Find the angle between the face diagonals of a cube.

Answer

\[ \begin{aligned} & \underline{A}=1 \hat{x}+0 \hat{y}+1 \hat{z} \\ & \underline{B}=0 \hat{x}+1 \hat{y}+1 \hat{z} \\ & \underline{A} \cdot \underline{B}=1 \cdot 0+0 \cdot 1+1 \cdot 1=1 \end{aligned} \] also \[ \begin{aligned} & A \cdot \underline{B}=A B \cos \theta \\ & A=\sqrt{1^{2}+0^{2}+1^{2}}=\sqrt{2} \\ & B=\sqrt{O^{2}+1^{2}+1^{2}}=\sqrt{2} \\ & A \cdot B=\sqrt{2} \cdot \sqrt{2} \cos \theta \\ & =2 \cos \theta \\ & 1=2 \cos \theta \\ & \theta=\cos ^{-1}(1 / 2) \\ & \theta=60^{\circ} \text {. } \end{aligned} \]