6 Differentiation of vectors
Lets consider the derivative of \(\mathbf{a}(u)\) with respect to \(u\). The derivative of a vector is defined in a similar way to the derivative of a scaler. \[ \begin{aligned} \Delta \mathbf{a} = \mathbf{a}(u+\Delta u)-\mathbf{a}(u)\\ \\ \frac{d\mathbf{a}}{du} = \lim _{\Delta u \rightarrow 0} \frac{\mathbf{a}(u+\Delta u) - \mathbf{a}(u)}{\Delta u} \end{aligned} \] \(\frac{d\mathbf{a}}{du}\) is a vector. In Cartesian coordinates \[ \begin{aligned} & \text { if } \mathbf{a}=a_{x} \hat{\imath}+a_{y} \hat{\jmath}+a_{z} \hat{k} \\ \\ & \frac{d \mathbf{a}}{d u}=\frac{d a_{x}}{d u} \hat{\imath}+\frac{d a_{y}}{d u} \hat{\jmath}+\frac{d a_{z}}{d u} \hat{k}. \end{aligned} \]
Lets find the velocity of a particle \[ \begin{aligned} & \mathbf{r}(t)=x(t) \hat{\imath}+y(t) \hat{\jmath}+z(t) \hat{k} \\ \\ & \mathbf{v}(t)=\frac{d \mathbf{r}}{d t}=\frac{d x}{d t} \hat{\imath}+\frac{d y}{d t} \hat{\jmath}+\frac{d z}{d t} \hat{k} \end{aligned} \]
The direction of \(\mathbf{v}(t)\) is tangent to the path \(\mathbf{r}(t)\) and \(|\mathbf{v}(t)|\) is the speed of the particle. \[ \mathbf{a}(t)=\frac{d \mathbf{v}}{d t}=\frac{d^{2} x}{d t^{2}} \hat{\imath}+\frac{d^{2} y}{d \hat{t}^{2}} \hat{j}+\frac{d^{2} z}{d t^{2}} \hat{k} \]
\(\mathbf{r}(t) = 2 t^{2} \hat{\imath}+(3 t-2) \hat{\jmath}+\left(3 t^{2}-1\right) \hat{k}\) Find the speed of the particle at \(t=1\) and the component of its acceleration in the direction \(\mathbf{s} = \hat{\imath} + 2 \hat{j} + \hat{k}\).
\[ \begin{aligned} & \frac{d \mathbf{r}}{d t}=4 t \hat{\imath}+3 \hat{\jmath}+6 t \hat{k} \\ & v(1)=\sqrt{4^{2}+9+36} \\ & =\sqrt{61} \end{aligned} \]
Now lets find the acceleration: \(\mathbf{a}=4 \hat{\imath}+6 \hat{k}\) \(\mathbf{a}\) is independent of time.
To find the component of \(\mathbf{a}\) in the direction of \(\mathbf{s}\) we need to find the unit vector \(\hat{s}\) and project \(\mathbf{a}\) in that direction: \[ \mathbf{a} \cdot \hat{s}=(4 \hat{\imath}+6 \hat{k}) \cdot(\hat{\imath}+2 \hat{\imath}+\hat{k}) / \sqrt{6}=(4+0+6) / \sqrt{6} = 10/\sqrt{6} \]
6.1 Plane Polar Coordinates
What if another coordinate system is more appropriate?
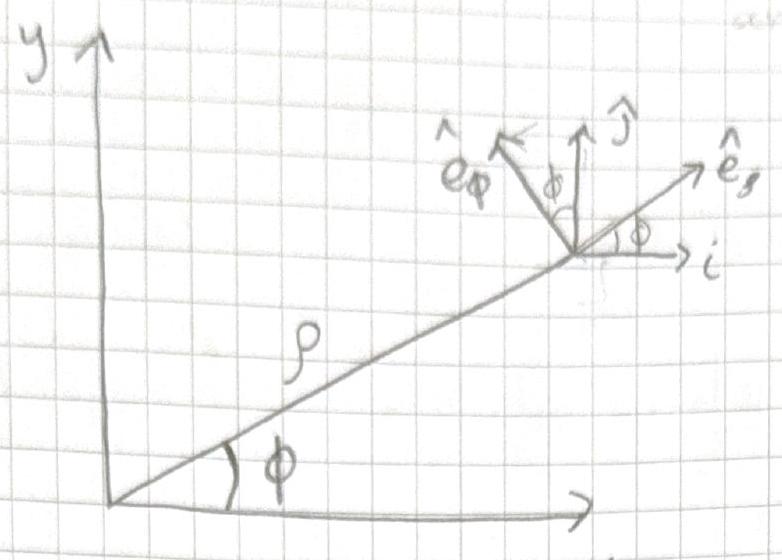
Lets start by writing the polar coordinates in terms of Cartesian \(\hat{i}+\hat{\jmath}\) \[ \begin{aligned} & \hat{e}_{\rho}=\cos \phi \hat{\imath}+\sin \phi \hat{\jmath} \\ & \hat{e}_{\phi}=-\sin \phi \hat{\imath}+\cos \phi \hat{\jmath} \\ & \frac{d \hat{e}_{\rho}}{d t}=-\sin \phi \frac{d \phi}{d t} \hat{\imath}+\cos \phi \frac{d \phi}{d t} \hat{\jmath} \\ & =\dot{\phi} \hat{e}_{\phi} \\ & \frac{d \hat{e}_\rho}{d t}=-\cos \phi \frac{d \phi}{d t} \hat{\imath}-\sin \phi \frac{d \phi}{d t} \hat{\jmath} \\ & \frac{d \hat{e}_{\rho}}{d t}=-\dot{\phi} \hat{e}_{\rho} \end{aligned} \]
The overdot is standard notation for a time derivative.
\(\mathbf{r}(t)=\rho(t) \hat{e}_\rho\). Find \(\mathbf{v}(t)\) and \(\mathbf{a}(t)\) in these coordinates.
\[ \begin{aligned} & \mathbf{v}(t)=\dot{\mathbf{r}}(t)=\dot{\rho} \hat{e}_{\rho}+\rho \dot{\hat{e}}_{\rho}=\dot{\rho} \hat{e}_{\rho}+\rho \dot{\phi} \hat{e}_{\phi} \\ & \mathbf{a}(t)=\frac{d}{d t}\left(\dot{\rho} \hat{e}_{\rho}+\rho \dot{\phi} {\hat{e}_\phi}\right) \\ & =\ddot{\rho} \hat{e}_{\rho}+\dot{\rho} \dot{\hat{e}}_{\rho}+\dot{\rho} \dot{\phi} \hat{e}_{\phi}+\rho \ddot{\phi} \hat{e}_{\phi}+\rho \dot{\phi} \dot{\hat{e}}_{\phi} \\ & =\ddot{\rho} \hat{e}_{\rho}+\dot{\rho} \dot{\phi} \hat{e}_{\phi}+\dot{\rho} \dot{\phi} \hat{e}_{\phi}+\rho \ddot{\phi} \hat{e}_{\phi}-\rho \dot{\phi}^{2} \hat{e}_\rho \\ & =\left(\ddot{\rho}-\rho \dot{\phi}^{2}\right) \hat{e}_{\rho}+(2 \dot{\rho} \dot{\phi}+\rho \ddot{\phi}) \hat{e}_{\phi} \end{aligned} \]
6.2 Differentiation of composite vector expressions
Lets consider a scalar \(\phi\) and a vectors \(\mathbf{a}\) and \(\mathbf{b}\). \[ \begin{aligned} & \frac{d}{d u}(\phi \mathbf{a})=\phi \frac{d \mathbf{a}}{d u}+\frac{d \phi}{d u} \mathbf{a} \\ & \frac{d}{d u}(\mathbf{a} \cdot \mathbf{b})=\mathbf{a} \cdot \frac{d \mathbf{b}}{d u}+\frac{d \mathbf{a}}{d u} \cdot \mathbf{b} \\ & \frac{d}{d u}(\mathbf{a} \times \mathbf{b})=\mathbf{a} \times \frac{d \mathbf{b}}{d u}+\frac{d \mathbf{a}}{d u} \times \frac{\mathbf{b}}{d u} \end{aligned} \]
A particle of mass \(m\) with position vector \(\mathbf{r}\) relative to some origin \(O\) experiences a force \(\mathbf{F}\) which produces a torque (moment) \(\mathbf{T}=\mathbf{v} \times \mathbf{F}\) about \(O\). The angular momentum is given by \(\mathbf{L}=\mathbf{r} \times m \mathbf{v}\). Show that the time rate of change angular momentum \(\frac{d \mathbf{L}}{d t}=\mathbf{T}\)
\[ \begin{aligned} & \frac{d L}{d t}=\frac{d}{d t}(r \times m v) \\ &=\left(r \times m \frac{d v}{d t}+\frac{d r}{d t} \times m \underline{v}\right) \\ &=v \times m \underline{v}+r \times m \frac{d v}{d t} \\ &=0+r \times E \\ & \prime_{r} \frac{d L}{d t}=I \end{aligned} \]